No CrossRef data available.
Article contents
Special curves in modular surfaces
Part of:
Diophantine approximation, transcendental number theory
Discontinuous groups and automorphic forms
Published online by Cambridge University Press: 02 December 2021
Abstract
We show that geodesics in
$\mathbf {H}$
attached to a maximal split torus or a real quadratic torus in
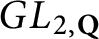$GL_{2, \mathbf {Q}}$
are the only irreducible algebraic curves in
$\mathbf {H}$
whose image in
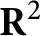$\mathbf {R}^2$
via the j-invariant is contained in an algebraic curve.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society, 2021
Footnotes
The author’s research is supported by the ERC Grant 804176.
References
André, Y., Finitude des couples d’invariants modulaires singuliers sur une courbe algébrique plane non modulaire. J. Reine Angew. Math. 505(1998), 203–208.CrossRefGoogle Scholar
Bakker, B. and Tsimerman, J., Lectures on the Ax–Schanuel conjecture. In: Nicole, M.-H. (ed.), Arithmetic geometry of logarithmic pairs and hyperbolicity of moduli spaces. Hyperbolicity in Montréal. Based on three workshops, Montréal, Canada, 2018–2019, Springer, Cham, 2020, pp. 1–68.Google Scholar
Conrad, K., Ideal classes and matrix conjugation over Z. https://kconrad.math.uconn.edu/blurbs/gradnumthy/matrixconj.pdf.Google Scholar
Darmon, H. and Vonk, J., Arithmetic intersections of modular geodesics. J. Number Theory 230(2021), 89–111.CrossRefGoogle Scholar
Helgason, S., Differential geometry, Lie groups, and symmetric spaces, Pure and Applied Mathematics, 80, Academic Press, New York–San Francisco–London, 1978, 628 pp.Google Scholar
Jaffee, H. A., Real forms in Hermitian symmetric spaces and real algebraic varieties. 1974. https://www.math.stonybrook.edu/alumni/1974-Harris-Jaffee.pdf.Google Scholar
Klingler, B., Ullmo, E., and Yafaev, A.,
Bi-algebraic geometry and the André–Oort conjecture
. In: de Fernex, T., Hassett, B., Mustaţă, M., Olsson, M., Popa, M., Thomas, R. (ed.), Algebraic geometry: Salt Lake City 2015. Proceedings of the 2015 Summer Research Institute in Algebraic Geometry, University of Utah, Salt Lake City, UT, USA, July 13–31, 2015. Part 2, American Mathematical Society, Providence, RI; Clay Mathematics Institute, Cambridge, MA, 2018, pp. 319–359.Google Scholar
MathOverflow, Equations defining hyperbolic geodesics in
$\mathbb{C}\, \setminus \, \lbrace 0,1\rbrace $
2020. https://mathoverflow.net/questions/375352/equations-defining-hyperbolic-geodesics-in-mathbb-c-setminus-0-1 (MathOverflow post).Google Scholar
$\mathbb{C}\, \setminus \, \lbrace 0,1\rbrace $
2020. https://mathoverflow.net/questions/375352/equations-defining-hyperbolic-geodesics-in-mathbb-c-setminus-0-1 (MathOverflow post).Google ScholarPila, J., O-minimality and the André–Oort conjecture for ℂ
n
. Ann. of Math. 173(2011), no. 3, 1779–1840.CrossRefGoogle Scholar
Rickards, J., Computing intersections of closed geodesics on the modular curve. J. Number Theory 225(2021), 374–408.CrossRefGoogle Scholar
Sarnak, P., Reciprocal geodesics. In: Duke, W., Tschinkel, Y. (ed.), Analytic number theory. A tribute to Gauss and Dirichlet. Proceedings of the Gauss–Dirichlet conference, Göttingen, Germany, June 20–24, 2005, American Mathematical Society, Providence, RI, 2007, pp. 217–237.Google Scholar
Schneider, T., Arithmetische Untersuchungen elliptischer Integrale. Math. Ann. 113(1936), 1–13.CrossRefGoogle Scholar