Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Carroll, C. E.
1982.
Proof of Oppenheim's area inequalities for triangles and quadrilaterals.
Aequationes Mathematicae,
Vol. 24,
Issue. 1,
p.
97.
Mitrinović, D. S.
Pečarić, J. E.
and
Volenec, V.
1989.
Recent Advances in Geometric Inequalities.
p.
144.


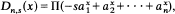 , where
, where 