Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T13:42:03.686Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Rings of Invariants that are Cohen-Macaulay

Published online by Cambridge University Press:  20 November 2018

Larry Smith
Larry Smith*
Affiliation:
Mathematisches Institut, der Universität Göttingen, Bunsenstrasse 3-5, D 37073 Göttingen, Germany, e-mail:[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

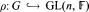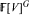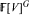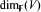Let be a representation of the finite group G over the field . If the order |G| of G is relatively prime to the characteristic of or n = 1 or 2, then it is known that the ring of invariants is Cohen-Macaulay. There are examples to show that need not be Cohen-Macaulay when |G| is divisible by the characteristic of . In all such examples is at least 4. In this note we fill the gap between these results and show that rings of invariants in three variables are always Cohen-Macaulay.

Keywords

13B99
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 39 , Issue 2 , 01 June 1996 , pp. 238 - 240
Copyright
Copyright © Canadian Mathematical Society 1996

References

1. Bertin, M. -J., Anneaux d'invariants d'anneaux de polynômes en caractéristique p, C. R. Acad. Sci. Paris (Série A) 277(1973), 691–694.Google Scholar
2. Campbell, H. E. A., Hughes, I. P. and Pollack, R. D., Rings of Invariants andp-Sylow Subgroups, Can. Math. Bull. 34(1991), 42–47.Google Scholar
3. Ellingsrud, G. and Skjelbred, T., Profondeur d'anneaux d'invariants en caractéristique p, Comp. Math. 41(1980), 233–244.Google Scholar
4. Fossum, R. M. and Griffith, P. A., Complete Local Factorial Rings which are not Cohen-Macaulay in characteristic p, Ann. Sci. École Norm. Sup. (4) 8(1975), 189–200.Google Scholar
5. Hochster, M. and Eagon, J. A., Cohen-Macaulay Rings, Invariant Theory, and the Generic Perfection of Determinantal Loci, Amer. J. of Math. 93(1971), 1020–1058.Google Scholar
6. Landweber, P S. and Stong, R. E., The Depth of Rings of Invariants over Finite Fields, Proc. New York Number Theory Seminar, 1984, Lecture Notes in Math. Springer, New York, 1987.Google Scholar
7. Smith, L., Polynomial Invariants of Finite Groups, Peters, A. K. Ltd., Wellesley, MA, 1995.Google Scholar