Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T04:12:09.566Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Results on the Domination Number of a Zero-divisor Graph

Published online by Cambridge University Press:  20 November 2018

Sima Kiani ,
Hamid Reza Maimani  and
Reza Nikandish
Sima Kiani
Affiliation:
Department of Mathematics, Science and Research Branch, Islamic Azad University, Tehran, Iran e-mail: [email protected]
Hamid Reza Maimani
Affiliation:
Mathematics Section, Department of Basic Sciences, Shahid Rajaee Teacher Training University, Tehran, Iran and School of Mathematics, Institute for Research in Fundamental Sciences (IPM), Tehran, Iran e-mail: [email protected]
Reza Nikandish
Affiliation:
Department of Mathematics, Jundi-Shapur University of Technology, Dezful, Iran and School of Mathematics, Institute for Research in Fundamental Sciences (IPM), Tehran, Iran e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we investigate the domination, total domination, and semi-total domination numbers of a zero-divisor graph of a commutative Noetherian ring. Also, some relations between the domination numbers of 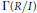$\Gamma \left( {R}/{I}\; \right)$ and 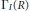${{\Gamma }_{1}}\left( R \right)$, and the domination numbers of 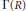$\Gamma \left( R \right)$ and 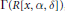$\Gamma \left( R\left[ x,\,\alpha ,\,\delta \right] \right)$, where 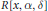$R\left[ x,\,\alpha ,\,\delta \right]$ is the Ore extension of 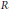$R$, are studied.

Keywords

05C7513H10zero-divisor graphdomination number
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 3 , 01 September 2014 , pp. 573 - 578
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Afkhami, M., Khashyarmanesh, K., and Khorsandi, M. R., Zero-divisor graphs of Ore extension rings. J. Algebra Appl. 10 (2011), no. 6, 1309–1317. http://dx.doi.org/10.1142/S0219498811005191 Google Scholar
[2] Anderson, D. F. and Livingston, P. S., The zero-divisor graph of a commutative ring. J. Algebra 217 (1999), no. 2, 434–447. http://dx.doi.org/10.1006/jabr.1998.7840 Google Scholar
[3] Annin, S., Associated primes over Ore extension rings. J. Algebra Appl. 3 (2004), no. 2, 193–205. http://dx.doi.org/10.1142/S0219498804000782 Google Scholar
[4] Beck, I., Coloring of commutative rings. J. Algebra 116 (1988), no. 1, 208–226. http://dx.doi.org/10.1016/0021-8693(88)90202-5 Google Scholar
[5] Jafari, N. Rad, Jafari, S. H., and Mojdeh, D. A., On domination in zero-divisor graphs. Canad. Math. Bull. 56 (2013), no. 2, 407–411. http://dx.doi.org/10.4153/CMB-2011-156-1 Google Scholar
[6] Maimani, H. R., Pournaki, M. R., Tehranian, A., and Yassemi, S., Graphs attached to rings revisited. Arab. J. Sci. Eng. 36 (2011), no. 6, 997–1011. http://dx.doi.org/10.1007/s13369-011-0096-y Google Scholar
[7] Maimani, H. R., Pournaki, M. R., and Yassemi, S., Zero-divisor graph with respect to an ideal. Comm. Algebra 34 (2006), no. 3, 923–929. http://dx.doi.org/10.1080/00927870500441858 Google Scholar
[8] Mojdeh, D. A. and Rahimi, A. M., Dominating sets of some graphs associated to commutative rings. Comm. Algebra 40 (2012), no. 9, 3389–3396. http://dx.doi.org/10.1080/00927872.2011.589091 Google Scholar
[9] Nielsen, P. P., Semi-commutativity and the McCoy condition. J. Algebra 298 (2006), no. 1, 134–141. http://dx.doi.org/10.1016/j.jalgebra.2005.10.008 Google Scholar
[10] Redmond, S. P., An ideal-based zero-divisor graph of a commutative ring. Comm. Algebra 31 (2003), no. 9, 4425–4443. http://dx.doi.org/10.1081/AGB-120022801 Google Scholar
[11] Sharp, R. Y., Steps in commutative algebra. London Mathematical Society Student Texts, 19, Cambridge University Press, Cambridge, 1990.Google Scholar