Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T01:59:13.091Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Questions about Semisimple Lie Groups Originating in Matrix Theory

Published online by Cambridge University Press:  20 November 2018

Dragomir Ž. Ðoković  and
Tin-Yau Tam
Dragomir Ž. Ðoković
Affiliation:
Department of Pure Mathematics University of Waterloo Waterloo, Ontario N2L 3G1, email: [email protected]
Tin-Yau Tam
Affiliation:
Department of Mathematics Auburn University AL 36849—5310 USA, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We generalize the well-known result that a square traceless complex matrix is unitarily similar to a matrix with zero diagonal to arbitrary connected semisimple complex Lie groups 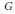$G$ and their Lie algebras 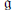$\mathfrak{g}$ under the action of a maximal compact subgroup $K$ of 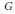$G$. We also introduce a natural partial order on 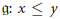$\mathfrak{g}:\,x\,\le y$ if 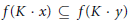$f(K\,\cdot \,x)\,\subseteq \,f(K\,\cdot \,y)$ for all 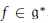$f\,\in \,{{\mathfrak{g}}^{*}}$, the complex dual of 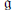$\mathfrak{g}$. This partial order is $K$-invariant and induces a partial order on the orbit space 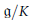$\mathfrak{g}/K$. We prove that, under some restrictions on 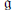$\mathfrak{g}$, the set 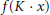$f(K\,\cdot \,x)$ is star-shaped with respect to the origin.

Keywords

15A4520G2022E60
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 3 , 01 September 2003 , pp. 332 - 343
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Au-Yeung, Y. H. and Sing, F. Y., A remark on the generalized numerical range of a normal matrix. Glasgow Math. J. 18 (1977), 179–180.Google Scholar
[2] Bourbaki, N., Groupes et algèbres de Lie, Chapitres 4, 5 et 6. Hermann, Paris, 1968.Google Scholar
[3] Bourbaki, N., Groupes et algèbres de Lie, Chapitres 7 et 8. Hermann, Paris, 1975.Google Scholar
[4] Cheung, W. S. and Tsing, N. K., The C-numerical range of matrices is star-shaped. Linear and Multilinear Algebra 41 (1996), 245–250.Google Scholar
[5] Helgason, S., Differential Geometry, Lie Groups, and Symmetric Spaces. Academic Press, New York, 1978.Google Scholar
[6] Horn, R. A. and Johnson, C. R., Topics in Matrix Analysis. Cambridge University Press, 1991.Google Scholar
[7] Humphreys, J. E., Introduction to Lie Algebras and Representation Theory. Springer-Verlag, New York 1972.Google Scholar
[8] Li, C. K., Some convexity theorems for the generalized numerical ranges. Linear and Multilinear Algebra 40 (1996), 235–240.Google Scholar
[9] Murnaghan, F. D., On the unitary invariants of a square matrix. Anais Acad. Brasil. Ci. 26 (1954), 1–7.Google Scholar
[10] Nakazato, H., The C-numerical range of a 2 × 2 matrix. Sci. Rep. Hirosaki Univ. 41 (1994), 197–206.Google Scholar
[11] Sibirskiĭ, K. S., The Algebraic Invariants of Differential Equations and Matrices. (Russian) Stiintsa, Kishinev, 1976.Google Scholar
[12] Tam, T. Y., On the shape of numerical range associated with Lie groups. Taiwanese J. Math. 5 (2001), 497–506.Google Scholar