Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-22T05:17:04.036Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Properties of Indicatrices in a Finsler Space(1)

Published online by Cambridge University Press:  20 November 2018

T. N. Srivastava  and
Shôji Watanabe
T. N. Srivastava
Affiliation:
Department of Mathematics, Concordia University (Loyola Campus), 7141, Sherbrooke Street West, Montreal, Quebec, Canada
Shôji Watanabe
Affiliation:
Department of Mathematics, Concordia University (Loyola Campus), 7141, Sherbrooke Street West, Montreal, Quebec, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (Mn, F) be an n-dimensional Finsler space where Mn is the underlying n-dimensional manifold and 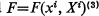is the Finsler fundamental function. F being a differentiable function of the point 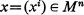and element of support 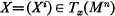where T∞(Mn) is the tangent space of Mn at x and is positively homogeneous of degree one with respect to X.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 18 , Issue 5 , 01 December 1975 , pp. 715 - 721
Copyright
Copyright © Canadian Mathematical Society 1975

Footnotes

Dedicated to Prof. J. Kanitani on the occasion of his 80th birthday.

(2)

Permanent Address: Department of Mathematics, Science University of Tokyo, Tokyo, Japan.

(1)

This work was supported in part by the National Research Council of Canada under grant #A8788 and in part be the Science University of Tokyo.

References

1. Kikuchi, S., Theory of Minkowski space and of non-linear connections in Finsler space, Tensor N.S., 12 (1962), 47-60.Google Scholar
2. Rund, H., The differential geometry of Finsler spaces, Springer-Verlag (1959).Google Scholar
3. Watanabe, S., On indicatrices of a Finsler space, Tensor N.S., 27 (1973), 135-137.Google Scholar
4. Yano, K., Integral formulas in Riemannian geometry, Marcel Dekker (1970).Google Scholar