Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T09:59:36.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Norm Inequalities for Operators

Published online by Cambridge University Press:  20 November 2018

Fuad Kittaneh
Fuad Kittaneh*
Affiliation:
Department of Mathematics University of Jordan Amman Jordan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

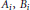Let ${{A}_{i}},\,{{B}_{i}}$ and 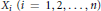${{X}_{i}}\,(i\,=\,1,\,2,\ldots ,\,n)$ be operators on a separable Hilbert space. It is shown that if 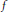$f$ and $g$ are nonnegative continuous functions on 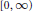$\left[ 0,\infty \right)$ which satisfy the relation 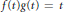$f\,(t)g(t)\,=\,t$ for all $t$ in 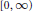$\left[ 0,\infty \right)$, then

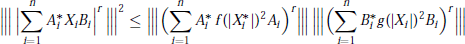$${{\left\| \left| \,{{\left| \sum\limits_{i=1}^{n}{A_{i}^{*}{{X}_{i}}{{B}_{i}}} \right|}^{r}} \right| \right\|}^{2}}\,\le \,\left\| \left| {{\left( \sum\limits_{i=1}^{n}{A_{i}^{*}f{{(\left| X_{i}^{*} \right|)}^{2}}{{A}_{i}}} \right)}^{r}} \right| \right\|\,\,\left\| \left| {{\left( \sum\limits_{i=1}^{n}{B_{i}^{*}g{{(\left| {{X}_{i}} \right|)}^{2}}\,{{B}_{i}}} \right)}^{r}} \right| \right\|$$

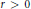for every $r\,>\,0$ and for every unitarily invariant norm. This result improves some known Cauchy-Schwarz type inequalities. Norm inequalities related to the arithmetic-geometric mean inequality and the classical Heinz inequalities are also obtained.

Keywords

47A3047B1047B1547B20unitarily invariant normpositive operatorarithmetic-geometric mean inequalityCauchy-Schwarz inequalityHeinz inequality
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 1 , 01 March 1999 , pp. 87 - 96
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Andruchow, E., Corach, G. and Stojanoff, D., Geometric operator inequalities. Linear Algebra Appl. 258 (1997), 295–310.Google Scholar
[2] Bhatia, R., Perturbation inequalities for the absolute value map in norm ideals of operators. J. Operator Theory 19 (1988), 129–136.Google Scholar
[3] Bhatia, R., A simple proof of an operator inequality of Jocić and Kittaneh. J. Operator Theory 31 (1994), 21–22.Google Scholar
[4] Bhatia, R. and Davis, C., More matrix forms of the arithmetic-geometric mean inequality. SIAMJ. Matrix Anal. Appl. 14 (1993), 132–136.Google Scholar
[5] Bhatia, R. and Davis, C., A Cauchy-Schwarz inequality for operators with applications. Linear Algebra Appl. 223/224 (1995), 119–129.Google Scholar
[6] Bhatia, R. and Holbrook, J. A. R., On the Clarkson-McCarthy inequalities. Math. Ann. 281 (1988), 7–12.Google Scholar
[7] Bhatia, R. and Kittaneh, F., On the singular values of a product of operators. SIAM J. Matrix Anal. Appl. 11 (1990), 272–277.Google Scholar
[8] Bhatia, R. and Kittaneh, F., Norm inequalities for partitioned operators and an application. Math. Ann. 287 (1990), 719–726.Google Scholar
[9] Fujii, J. I., Fujii, M., Furuta, T. and Nakamoto, R., Norm inequalities equivalent to the Heinz inequality. Proc. Amer. Math. Soc. 118 (1993), 827–830.Google Scholar
[10] Furuta, T., A note on the arithmetic-geometric mean inequality for every unitarily invariant matrix norm. Linear Algebra Appl. 208/209 (1994), 223–228.Google Scholar
[11] Gohberg, I. C. and Krein, M. G., Introduction to the theory of linear nonself-adjoint operators. Transl. Math. Monographs 18, Amer.Math. Soc., Providence, RI, 1969.Google Scholar
[12] Heinz, E., Beiträge zur Störungstheorie der Spektralzerlegung. Math. Ann. 123 (1951), 415–438.Google Scholar
[13] Horn, R. A. and Mathias, R., An analog of the Cauchy-Schwarz inequality for Hadamard products and unitarily invariant norms. SIAM J. Matrix Anal. Appl. 11 (1990), 481–498.Google Scholar
[14] Horn, R. A., Cauchy-Schwarz inequalities associated with positive semidefinite matrices. Linear Algebra Appl. 142 (1990), 63–82.Google Scholar
[15] Horn, R. A., Norm bounds for Hadamard products and an arithmetic-geometric mean inequality for unitarily invariant norms. Linear Algebra Appl. 223/224 (1995), 355–361.Google Scholar
[16] Jocić, D. and Kittaneh, F., Some perturbation inequalities for self-adjoint operators. J. Operator Theory 31 (1994), 3–10.Google Scholar
[17] Kato, T., A generalization of the Heinz inequality. Proc. Japan Acad. 37 (1961), 305–308.Google Scholar
[18] Kittaneh, F., Notes on some inequalities for Hilbert space operators. Publ. Res. Inst. Math. Sci. 24 (1988), 283–293.Google Scholar
[19] Kittaneh, F., A note on the arithmetic-geometric mean inequality for matrices. Linear Algebra Appl. 171 (1992), 1–8.Google Scholar
[20] Kittaneh, F., Norm inequalities for fractional powers of positive operators. Lett. Math. Phys. 27 (1993), 279–285.Google Scholar
[21] Kittaneh, F., On some operator inequalities. Linear Algebra Appl. 208/209 (1994), 19–28.Google Scholar
[22] Mathias, R., An arithmetic-geometric mean inequality involving Hadamard products. Linear Algebra Appl. 184 (1993), 71–78.Google Scholar
[23] McIntosh, A., Heinz inequalities and perturbation of spectral families. Macquarie Mathematics Reports 79- 0006, Macquarie University, 1979.Google Scholar
[24] Schatten, R., Norm ideals of completely continuous operators. Springer-Verlag, Berlin, 1960.Google Scholar
[25] Simon, B., Trace ideals and their applications. Cambridge University Press, Cambridge, 1979.Google Scholar
[26] Simon, B., Convergence in trace ideals. Proc. Amer.Math. Soc. 83 (1981), 39–43.Google Scholar