Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-16T16:17:22.738Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Inequalities Related to the Wald-Wolfowitz-Noether Condition*

Published online by Cambridge University Press:  20 November 2018

K. L. Mehra  and
J. S. W. Wong
K. L. Mehra
Affiliation:
University of Alberta, (Edmonton)
J. S. W. Wong
Affiliation:
University of Alberta, (Edmonton)
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If {avα: or = 1, 2, …, N }, with Nv → ∞ as v → ∞, is a double sequence of real numbers with the property that 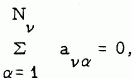, then

1.1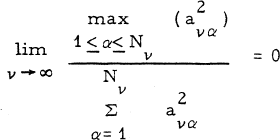

is known in statistical literature as the Wald- Wolfowitz- Noether condition and it plays an important role in the proofs of certain types of central limit theorems (see e. g., [ l ], [2] ).

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 9 , Issue 2 , June 1966 , pp. 161 - 169
Copyright
Copyright © Canadian Mathematical Society 1966

Footnotes

*

This work was done while the authors were attending the summer Institute of the Canadian Mathematical Congress, Vancouver, 1965.

References

1. Hȥjek, J., Some extensions of the Wald-Wolf owitz-Noether Theorem, Ann. Math, Statist. 32 (1961), 506-523.Google Scholar
2. Mehra, K. L., On some multi- treatment rank-order tests for experiments involving paired-observations, Ann. Math. Statist., (to appear).Google Scholar
3. Loéve, M., Probability Theory, (Second Edition, 1960), Van Nostrand, New York.Google Scholar
4. Wong, J.S.W., Remarks on a result of Gram Determinants and generalized Schwartz Inequality, The Matrix and Tensor Quarterly, 8 (1964), 77-80.Google Scholar