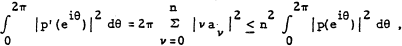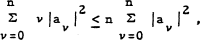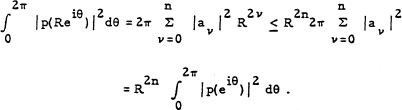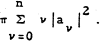Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Durand, A.
1990.
Cinquante Ans de Polynômes Fifty Years of Polynomials.
Vol. 1415,
Issue. ,
p.
43.
Dewan, K.K.
Bhat, Aijaz Ahmad
and
Pukhta, Mohammad Sayeed
1998.
Inequalities Concerning theLp-Norm of a Polynomial.
Journal of Mathematical Analysis and Applications,
Vol. 224,
Issue. 1,
p.
14.


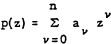 be a polynomial of degree n. Then clearly
be a polynomial of degree n. Then clearly