Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-25T05:07:26.839Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Generalizations of an Identity of Subhankulov

Published online by Cambridge University Press:  20 November 2018

D. Suryanarayana  and
David T. Walker
D. Suryanarayana
Affiliation:
Department of Mathematical Sciences Memphis State University, Memphis, Tennessee 38152
David T. Walker
Affiliation:
Department of Mathematical Sciences Memphis State University, Memphis, Tennessee 38152
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1957, M. A. Subhankulov established the following identity

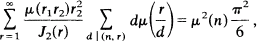
where 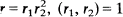; μ is the Môbius function and J2 is the Jordan totient function of order 2. Since the Ramanujan trigonometrical sum C(nr) = ∑d| (n, r)dμ(r/d), we rewrite the above identity using C(n, r).

In this paper, we give a generalization of Ramanujan's sum, which generalizes some of the earlier generalizations mainly due to E. Cohen, and prove a theorem from which we deduce some generalizations of the above identity.

Keywords

10A2010A99Möbius functionJordan totient functiongeneralized Ramanujan's sumk-free integersRiemann zeta function
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 20 , Issue 4 , 01 December 1977 , pp. 489 - 494
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. Cohen, E., An extension of Ramanujan's sum, Duke Math. J.,' 16 (1949), 85-90.Google Scholar
2. Cohen, E., Some totient functions, Duke Math. J., 23 (1956), 515-522.Google Scholar
3. Cohen, E., Generalizations of the Euler φ-function, Scripta Math., 23 (1957), 157-161.Google Scholar
4. Cohen, E., Trigonometric sums in elementary number theory, Amer. Math. Monthly, 66 (1959), 105-117.Google Scholar
5. Cohen, E., A class of arithmetical functions in several variables with applications to congruences, Trans. Amer. Math. Soc, 96 (1960), 355-381.Google Scholar
6. Cohen, E., A trigonometric sum, Math. Student, 28 (1960), 29-32.Google Scholar
7. Dickson, L.E., History of the theory of numbers, Vol. I, Chelsea Publishing Company, reprinted, 1952.Google Scholar
8. Hardy, G.H. and Wright, E.M., An introduction to the theory of numbers, Fourth edition, Oxford University Press, 1960.Google Scholar
9. Klee, V.L., A generalization ofEulefs function, Amer. Math. Monthly, 55 (1948), 358-359.Google Scholar
10. Subhankulov, M.A., Some asymptotic formulas in additive theory of numbers (Russian), Scientific Journal of the Tadzhik University, Vol. X, No. 4, (1957), 15-22.Google Scholar
11. Subhankulov, M.A. and Muhatarov, S.N., Representations of a number as a sum of two square-free numbers (Russian), Izv. Akad. Nauk UzSSR Ser. Fiz.-Mat. Nauk 1960, No. 4, 3-10.Google Scholar
12. Sugunamma, M., Eckford Cohen's generalizations of Ramanujan's trigonometrical sum C(n, r), Duke Math. J., 27 (1960), 323-330.Google Scholar