Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chvátal, V
1972.
Monochromatic paths in edge-colored graphs.
Journal of Combinatorial Theory, Series B,
Vol. 13,
Issue. 1,
p.
69.
Graham, R. L.
and
Kleitman, D. J.
1973.
Increasing paths in edge ordered graphs.
Periodica Mathematica Hungarica,
Vol. 3,
Issue. 1-2,
p.
141.
1973.
Graphs and Hypergraphs.
Vol. 6,
Issue. ,
p.
498.
1978.
Algorithmic Aspects of Combinatorics.
Vol. 2,
Issue. ,
p.
239.
Klee, Victor
1979.
Some Unsolved Problems in Plane Geometry.
Mathematics Magazine,
Vol. 52,
Issue. 3,
p.
131.
Chung, F.R.K
1980.
On unimodal subsequences.
Journal of Combinatorial Theory, Series A,
Vol. 29,
Issue. 3,
p.
267.
Berge, Claude
1982.
Diperfect graphs.
Combinatorica,
Vol. 2,
Issue. 3,
p.
213.
Berge, Claude
1984.
Topics on Perfect Graphs.
Vol. 88,
Issue. ,
p.
45.
Calderbank, A.R.
Chung, F.R.K.
and
Sturtevant, D.G.
1984.
Increasing sequences with nonzero block sums and increasing paths in edge-ordered graphs.
Discrete Mathematics,
Vol. 50,
Issue. ,
p.
15.
Moser, W. O. J.
1985.
PROBLEMS ON EXTREMAL PROPERTIES OF A FINITE SET OF POINTS.
Annals of the New York Academy of Sciences,
Vol. 440,
Issue. 1,
p.
52.
Pouzet, M.
1985.
Graphs and Order.
p.
592.
Tuza, Zs.
1989.
Irregularities of Partitions.
p.
141.
Graham, R. L.
and
Nešetřil, J.
1997.
The Mathematics of Paul Erdös II.
Vol. 14,
Issue. ,
p.
193.
Alon, Noga
2003.
Problems and results in extremal combinatorics—I.
Discrete Mathematics,
Vol. 273,
Issue. 1-3,
p.
31.
Mynhardt, C.M.
Burger, A.P.
Clark, T.C.
Falvai, B.
and
Henderson, N.D.R.
2005.
Altitude of regular graphs with girth at least five.
Discrete Mathematics,
Vol. 294,
Issue. 3,
p.
241.
Mynhardt, C.M.
2008.
Trees with depression three.
Discrete Mathematics,
Vol. 308,
Issue. 5-6,
p.
855.
Gaber-Rosenblum, Iris
and
Roditty, Yehuda
2009.
The depression of a graph and the diameter of its line graph.
Discrete Mathematics,
Vol. 309,
Issue. 6,
p.
1774.
Katrenič, J.
and
Semanišin, G.
2010.
Finding monotone paths in edge-ordered graphs.
Discrete Applied Mathematics,
Vol. 158,
Issue. 15,
p.
1624.
Mynhardt, C.M.
and
Schurch, M.
2013.
A class of graphs with depression three.
Discrete Mathematics,
Vol. 313,
Issue. 11,
p.
1224.
Graham, Ron L.
and
Nešetřil, Jaroslav
2013.
The Mathematics of Paul Erdős II.
p.
171.


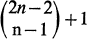 points in the plane one can always choose
points in the plane one can always choose 