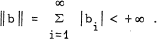Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-25T04:07:34.173Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Characterizations of co and ℓ1

Published online by Cambridge University Press:  20 November 2018

J. R. Retherford
J. R. Retherford*
Affiliation:
The Louisiana State University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The space co consists of the sequences tending to zero with addition and scalar multiplication defined coordinate-wise and with the sup norm. The space ℓ1 consists of the sequences b = (bi) under coordinate»wise arithmetic for which

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 10 , Issue 1 , April 1967 , pp. 39 - 52
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Abdelhay, José, Caracterisations de l′space de Banach de toutes les suites de nombresréelstendantvers zero. C. R. Acad. Sci. Paris 229 (1944), pages 1111-1112.Google Scholar
2. Arsove, M. G., Similar Bases and Isomorphisms in Frechét spaces. Math. Annalen, 135 (1955), pages 283-293.CrossRefGoogle Scholar
3. Arsove, M. G. and Edwards, R. E., Generalized Bases in topological linear spaces. Studi. Math. 19 (1966), pages 95-113.Google Scholar
4. Banach, S., Théorie des operations linéaires. Monografje Matematycyne, Warszawa (1933).Google Scholar
5. Bessaga, C. and Pelczynski, A., On bases and unconditional convergence of series in Banach spaces. Studi. Math. 17 (1955), pages 151-164.Google Scholar
6. Bessaga, C. and Pelczynski, A., A generalization of results of R. C. James concerning absolute bases in Banach spaces. Studi. Math. 17 (1955), pages 165-174.Google Scholar
7. Day, M. M., Normed linear spaces. Springer-Verlag, Berlin (1955).Google Scholar
8. Grinblyum, M. M., On the representation of a space of the type B in the form of a direct sum of subspaces. Dokl. Akad. Nauk. SSSR (U. S.) 70 (1955), pages 749-752 (in Russian).Google Scholar
9. Jones, O. T. and Retherford, J. R., On Similar Bases in Barrelled spaces, (to appear in Proc. Am. Math, Soc.)Google Scholar
10. Kelley, J. L., Namioka, I., et. al., Linear Topological spaces. New York, (1966).Google Scholar
11. Singer, I., Basic sequences and reflexivity of Banach spaces. Studi. Math. 21 (1966), pages 351-372.Google Scholar
12. Taylor, A. E., Introduction to Functional Analysis. New York (1955).Google Scholar
13. Veic, B. E., Some characteristic properties of unconditional bases. Dokl. Akad. Nau. SSSR 155 (1966), pages 509-512 (in Russian).Google Scholar
14. Yamazaki, S., On Bases in-Banach Spaces. Sci. Papers. Coll. Gen. Ed. Univ. Tokyo, 10 (I960), pages 163-169.Google Scholar