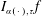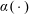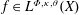Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ohno, Takao
and
Shimomura, Tetsu
2022.
Sobolev's inequality in central Herz-Morrey-Musielak-Orlicz spaces over metric measure spaces.
Complex Variables and Elliptic Equations,
Vol. 67,
Issue. 5,
p.
1154.
Hurri-Syrjänen, Ritva
Ohno, Takao
and
Shimomura, Tetsu
2023.
Trudinger’s Inequality on Musielak–Orlicz–Morrey Spaces Over Non-doubling Metric Measure Spaces.
Mediterranean Journal of Mathematics,
Vol. 20,
Issue. 3,
Ohno, Takao
and
Shimomura, Tetsu
2024.
Trudinger‐type inequalities for variable Riesz potentials of functions in Musielak–Orlicz–Morrey spaces over metric measure spaces.
Mathematische Nachrichten,
Vol. 297,
Issue. 4,
p.
1248.