Hostname: page-component-f554764f5-68cz6 Total loading time: 0 Render date: 2025-04-10T22:06:32.305Z Has data issue: false hasContentIssue false
  • English
  • Français

Small Zeros of Quadratic Forms Avoiding a Finite Number of Prescribed Hyperplanes

Published online by Cambridge University Press:  20 November 2018

Rainer Dietmann
Rainer Dietmann*
Affiliation:
Institut für Algebra und Zahlentheorie, Pfaffenwaldring 57, D-70550 Stuttgart, Germany e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a new upper bound for the smallest zero 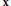$x$ of a quadratic form over a number field with the additional restriction that 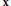$x$ does not lie in a finite number of 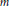$m$ prescribed hyperplanes. Our bound is polynomial in the height of the quadratic form, with an exponent depending only on the number of variables but not on 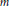$m$.

Keywords

11D0911E1211H4611H55
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 1 , 01 March 2009 , pp. 63 - 65
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Bombieri, E. and Vaaler, J., On Siegel's lemma. Invent. Math. 73(1983), no. 1, 11–32.Google Scholar
[2] Cassels, J. W. S., Bounds for the least solutions of homogeneous quadratic equations. Proc. Cambridge Philos. Soc. 51(1955), 262–264.Google Scholar
[3] Cassels, J. W. S., Rational quadratic forms. London Mathematical SocietyMonographs 13, Academic Press, London-New York, 1978.Google Scholar
[4] Fukshansky, L., Small zeros of quadratic forms with linear conditions. J. Number Theory 108(2004), no. 1, 29–43.Google Scholar
[5] Lang, S., Fundamentals of Diophantine geometry. Springer-Verlag, New York, 1983.Google Scholar
[6] Masser, D. W., How to solve a quadratic equation in rationals. Bull. London Math. Soc. 30(1998), no. 1, 24–28.Google Scholar
[7] Vaaler, J. D., Small zeros of quadratic forms over number fields. Trans. Amer. Math. Soc. 302(1987), no. 1, 281–296.Google Scholar