Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T10:24:35.588Z Has data issue: false hasContentIssue false
  • English
  • Français

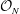Slow Continued Fractions and Permutative Representations of ${\mathcal{O}}_{N}$

Part of: Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  03 January 2020

Christopher Linden
Christopher Linden*
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, Urbana, IL, USA Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Representations of the Cuntz algebra 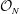${\mathcal{O}}_{N}$ are constructed from interval dynamical systems associated with slow continued fraction algorithms introduced by Giovanni Panti. Their irreducible decomposition formulas are characterized by using the modular group action on real numbers, as a generalization of results by Kawamura, Hayashi, and Lascu. Furthermore, a certain symmetry of such an interval dynamical system is interpreted as a covariant representation of the 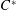$C^{\ast }$-dynamical system of the “flip-flop” automorphism of 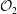${\mathcal{O}}_{2}$.

Keywords

Cuntz algebracontinued fractionspermutatative representationprojective linear groupMöbius transformation

MSC classification

Secondary: 11J70: Continued fractions and generalizations 39B12: Iteration theory, iterative and composite equations
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 4 , December 2020 , pp. 787 - 801
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, R. and Flatto, L., Geodesic flows, interval maps, and symbolic dynamics. Bull. Amer. Math. Soc. 25(1991), 229–335. https://doi.org/10.1090/s0273-0979-1991-16076-3CrossRefGoogle Scholar
Appelgate, H. and Onishi, H., The slow continued fraction algorithm via 2 × 2 integer matrices. American Mathematical Monthly 90(1983), 443–455. https://doi.org/10.2307/2975721Google Scholar
Archbold, R. J., On the ‘flip-flop’ automorphism of C ∗(S1, S2). Q. J. Math. 30(1979), 129–132. https://doi.org/10.1093/qmath/30.2.129CrossRefGoogle Scholar
Boca, F. P. and Merriman, C., Coding of geodesics on some modular surfaces and applications to odd and even continued fractions. Indag. Math. 29(2018), 1214–1234. https://doi.org/10.1016/j.indag.2018.05.004CrossRefGoogle Scholar
Boca, F. P. and Linden, C., On Minkowski type question mark functions associated with even or odd continued fractions. Monatsh. Math. 187(2018), 35–57. https://doi.org/10.1007/s00605-018-1205-8CrossRefGoogle Scholar
Bratteli, O. and Jorgensen, P. E. T., Iterated function systems and permutation representations of the Cuntz algebra. Mem. Amer. Math. Soc. 139(1999), no. 663, i–x, 1–89. https://doi.org/10.1090/memo/0663Google Scholar
Brown, G. and Yin, Q., Metrical theory for Farey continued fractions. Osaka J. Math. 33(1996), 951–970.Google Scholar
Cuntz, J., Simple C ∗-algebras generated by isometries. Comm. Math. Phys. 57(1977), 173–185. https://doi.org/10.1007/bf01625776CrossRefGoogle Scholar
Heersink, B., An effective estimate for the Lebesgue measure of preimages of iterates of the Farey map. Adv. Math. 291(2016), 621–634. https://doi.org/10.1016/j.aim.2016.01.003CrossRefGoogle Scholar
Hua, L. K., Introduction to number theory. Springer, Berlin Heidelberg, 1982. https://doi.org/10.1007/978-3-642-68130-1Google Scholar
Kawamura, K., Hayashi, Y., and Lascu, D., Continued fraction expansions and permutative representations of the Cuntz algebra 𝓞∞. J. Number Theory 129(2009), 3069–3080. https://doi.org/10.1016/j.jnt.2009.06.003CrossRefGoogle Scholar
Kawamura, K., Lascu, D., and Coltescu, I., Jump transformations and an embedding of 𝓞∞ into 𝓞2. J. Math. Phys. 50(2009), 033501. https://doi.org/10.1063/1.3081386CrossRefGoogle Scholar
Panti, G., A general Lagrange theorem. Amer. Math. Monthly 116(2009), 70–74. https://doi.org/10.4169/193009709x469823CrossRefGoogle Scholar
Panti, G., Slow continued fractions, transducers, and the Serret theorem. J. Number Theory 185(2018), 121–143. https://doi.org/10.1016/j.jnt.2017.08.034CrossRefGoogle Scholar
Serret, J. A., Cours d’algèbre supérieure. Third ed., Gauthier-Villars, Paris, 1866.Google Scholar
Schweiger, F., Continued fractions with odd and even partial quotients. Arbeitsberichte Math. Institut Universität Salzburg 4(1982), 59–70.Google Scholar
Williams, D., Crossed products of C ∗- algebras. American Mathematical Society, Providence, RI, 2007. https://doi.org/10.1090/surv/134CrossRefGoogle Scholar
Zagier, D., Nombres de classes et fractions continues. Astérisque 24–25(1975), 81–97.Google Scholar