Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T17:12:33.340Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular Riemannian Structures Compatible with π-Structures

Published online by Cambridge University Press:  20 November 2018

K. L. Duggal
K. L. Duggal*
Affiliation:
University of Windsor, Windsor, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

G. Legrand [1] studied a generalization of the almost complex structures [2] by considering a linear operator J acting on the complexified space of a differentiable manifold Vm satisfying a relation of the form J2 = λ2 (identity) where λ is a nonzero complex constant. Such structures are called π-structures. A π-structure is defined on Vm by the knowledge of two fields, of proper supplementary subspaces T1 and T2 of the complexified tangent space 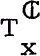at x ∈ Vm, such that dim(T1) = n1; dim(T2) = n2; n1 + n2 = m. In the remaining case, λ= 0, H. A. Eliopoulos [3] introduced almost tangent structures and discussed euclidean structures compatible with almost tangent structures [4]. In a similar way the purpose of this paper is to study singular riemannian structures compatible with π structures, briefly Rπ-structures.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 12 , Issue 6 , December 1969 , pp. 705 - 719
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Legrand, G., Etude d'une généralization des structures presque complexes sur les variétés différentiables Théses; Rendiconti del circolo Matematico di Palermo; (2) 7 (1958) 323–354, (2) 8 (1959) 5–48.Google Scholar
2. Lichnerowicz, A., Théorie globale des connexions et des groupes d' holonomie. (Edizioni Cremonese, Roma, 1962).Google Scholar
3. Eliopoulos, H. A., On the general theory of differentiable manifolds with almost tangent structures. Canad. Math. Bull. 8 (1965) 721–748.Google Scholar
4. Eliopoulos, H.A., Euclidean structures compatible with almost tangent structures. Bull, de I'Acad. Roy. de Belgique (5) 50 (1964) 1174–1182.Google Scholar
5. Bernard, D., Sur la géométrie différentielle des G-structures. Ann. Inst. Fourier 10 (1960) 153–273.Google Scholar
6. Steenrod, N., The topology of fibre bundles. (Princeton, 1951).Google Scholar
7. Chevalley, C., Theory of Lie groups. (Princeton, 1946).Google Scholar
8. Frolicher, A. and Nijenhuis, A., Theory of vector-valued differential forms, Part 1. K. Ned. Akad. Wet. Proc. Math Sc. 59 (1956) 338–359.Google Scholar
9. Eckmann, B., Structures complexes et transformations infinitésimales. Convegno Internazionale Di Geometria Differenziale. (Venice, 1953. Edizione Cremonese, Roma) (1954) 176–184.Google Scholar