Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T23:18:26.224Z Has data issue: false hasContentIssue false
  • English
  • Français

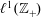Simplicial (Co)-homology of $\ell ^{1}(\mathbb{Z}_{+})$

Part of: Topological algebras, normed rings and algebras, Banach algebras Abstract harmonic analysis Homological methods

Published online by Cambridge University Press:  17 December 2018

Yasser Farhat  and
Frédéric Gourdeau
Yasser Farhat
Affiliation:
Academic Support Department, Abu Dhabi Polytechnic, P.O. Box 111499, Abu Dhabi, UAE Email: [email protected]
Frédéric Gourdeau
Affiliation:
Département de mathématiques et de statistique, Université Laval, 1045, avenue de la Médecine, Québec, QC G1V 0A6 Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the unital Banach algebra 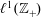$\ell ^{1}(\mathbb{Z}_{+})$ and prove directly, without using cyclic cohomology, that the simplicial cohomology groups 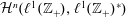${\mathcal{H}}^{n}(\ell ^{1}(\mathbb{Z}_{+}),\ell ^{1}(\mathbb{Z}_{+})^{\ast })$ vanish for all 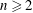$n\geqslant 2$. This proceeds via the introduction of an explicit bounded linear operator which produces a contracting homotopy for 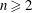$n\geqslant 2$. This construction is generalised to unital Banach algebras 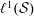$\ell ^{1}({\mathcal{S}})$, where 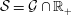${\mathcal{S}}={\mathcal{G}}\cap \mathbb{R}_{+}$ and 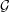${\mathcal{G}}$ is a subgroup of 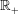$\mathbb{R}_{+}$.

Keywords

simplicial homologyBanach algebrasimplicial cohomology

MSC classification

Primary: 46H20: Structure, classification of topological algebras
Secondary: 43A20: $L^1$-algebras on groups, semigroups, etc. 16E40: (Co)homology of rings and algebras (e.g. Hochschild, cyclic, dihedral, etc.)
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 4 , December 2019 , pp. 756 - 766
Copyright
© Canadian Mathematical Society 2018 

Footnotes

This work was partially supported by the National Sciences and Engineering Research Council of Canada.

References

Bade, W. G., Curtis, P. C. Jr., and Dales, H. G., Amenability and weak amenability for Beurling and Lipschitz algebras . Proc. Lond. Math. Soc. 55(1987), 359–377. https://doi.org/10.1093/plms/s3-55_2.359 Google Scholar
Choi, Y., Gourdeau, F., and White, M. C., Simplicial cohomology of band semigroup algebras . Proc. Roy. Soc. Edinburgh Sect. A 142(2012), no. 4, 715–744. https://doi.org/10.1017/S0308210510000648 Google Scholar
Dales, H. G. and Duncan, J., Second order cohomology in groups of some semigroup algebras . In: Banach Algebras ’97 . Walter de Gruyter, Berlin, 1998, pp. 101–117.Google Scholar
Farhat, Y., Homologie et cohomologie de quelques algèbres de Banach. Ph.D. thesis, Université Laval, Québec, QC, 2013.Google Scholar
Gourdeau, F., Johnson, B. E., and White, M. C., The cyclic and simplicial cohomology of l 1(ℕ) . Trans. Amer. Math. Soc. 357(2005), no. 12, 5097–5113.Google Scholar
Gourdeau, F. and White, M. C., Vanishing of the third simplicial cohomology group of l 1(ℤ+) . Trans. Amer. Math. Soc. 353(2001), no. 5, 2003–2017.Google Scholar
Gourdeau, F. and White, M. C., The cyclic and simplicial cohomology of the bicyclic semigroup algebra . Q. J. Math. 62(2011), 607–624. https://doi.org/10.1093/qmath/haq014 Google Scholar
Gourdeau, F. and White, M. C., The cyclic and simplicial cohomology of the Cuntz semigroup algebra . J. Math. Anal. Appl. 386(2012), no. 2, 921–932. https://doi.org/10.1016/j.jmaa.2011.08.050 Google Scholar
Helemskii, A. Ya., Banach cyclic (co)homology and the Connes–Tzygan exact sequence . J. Lond. Math. Soc. 46(1992), 449–462. https://doi.org/10.1112/jlms/s2-46.3.449 Google Scholar