Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T12:05:07.990Z Has data issue: false hasContentIssue false
  • English
  • Français

A Short Proof of Paouris' Inequality

Published online by Cambridge University Press:  20 November 2018

Radosław Adamczak ,
Rafał Latała ,
Alexander E. Litvak ,
Krzysztof Oleszkiewicz ,
Alain Pajor  and
Nicole Tomczak-Jaegermann
Radosław Adamczak
Affiliation:
Institute of Mathematics, University of Warsaw, Banacha 2, 02-097 Warszawa, Poland e-mail: [email protected]@mimuw.edu.pl
Rafał Latała
Affiliation:
Institute of Mathematics, University of Warsaw, Banacha 2, 02-097 Warszawa, Poland e-mail: [email protected]@mimuw.edu.pl
Alexander E. Litvak
Affiliation:
Department of Mathematics and Statistical Sciences, University of Alberta, Edmonton, AB T6G 2G1 e-mail: [email protected]@mimuw.edu.pl
Krzysztof Oleszkiewicz
Affiliation:
Institute of Mathematics, University of Warsaw, Banacha 2, 02-097 Warszawa, Poland e-mail: [email protected]@mimuw.edu.pl
Alain Pajor
Affiliation:
Université Paris-Est, Équipe d'Analyse et Mathématiques Appliquées, 5, boulevard Descartes, Champs sur Marne, 77454 Marne-la-Vallée, Cedex 2, France e-mail: [email protected]@univ-mlv.fr
Nicole Tomczak-Jaegermann
Affiliation:
Department of Mathematics and Statistical Sciences, University of Alberta, Edmonton, AB T6G 2G1 e-mail: [email protected]@mimuw.edu.pl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

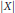We give a short proof of a result of G. Paouris on the tail behaviour of the Euclidean norm $\left| X \right|$ of an isotropic log-concave random vector 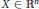$X\,\in \,{{\mathbb{R}}^{n}},$ stating that for every 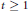$t\,\ge \,1$,

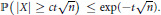$$\mathbb{P}\left( \left| X \right|\,\ge \,ct\sqrt{n} \right)\,\le \,\exp (-t\sqrt{n}).$$

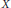More precisely we show that for any log-concave random vector $X$ and any 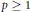$p\,\ge \,1$,

$${{(\mathbb{E}{{\left| X \right|}^{p}})}^{1/p}}\,\sim \,\mathbb{E}\left| X \right|\,+\,\underset{z\in {{S}^{n-1}}}{\mathop{\sup }}\,\,{{(\mathbb{E}{{\left| \left\langle z,\,X \right\rangle \right|}^{p}})}^{1/p}}.$$

Keywords

46B0646B0952A23log-concave random vectorsdeviation inequalities
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 1 , 14 March 2014 , pp. 3 - 8
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Adamczak, R., Guédon, O., Latała, R., Litvak, A. E., Oleszkiewicz, K., Pajor, A., and Tomczak-Jaegermann, N., Moment estimates for convex measures. arxiv:1207.6618 Google Scholar
[2] Adamczak, R., Latała, R., Litvak, A. E., Pajor, A., and Tomczak-Jaegermann, N., Tail estimates fornorms of sums of log-concave random vectors. arxiv:1107.4070. Google Scholar
[3] Adamczak, R., Geometry of log-concave ensembles of random matrices and approximate reconstruction. C. R. Math. Acad. Sci. Paris 349 (2011), no. 13–14, 783–786. http://dx.doi.org/10.1016/j.crma.2011.06.025 Google Scholar
[4] Barlow, R. E., Marshall, A.W., and Proschan, F., Properties of probability distributions with monotonehazard rate. Ann. Math. Statist. 34 (1963), 375–389. http://dx.doi.org/10.1214/aoms/1177704147 Google Scholar
[5] Borell, C., Convex measures on locally convex spaces. Ark. Mat. 12 (1974), 239–252. http://dx.doi.org/10.1007/BF02384761 Google Scholar
[6] Borell, C., Convex set functions in d-space. Period. Math. Hungar. 6 (1975), no. 2, 111–136. http://dx.doi.org/10.1007/BF02018814 Google Scholar
[7] Borell, C., The Brunn-Minkowski inequality in Gauss space. Invent. Math. 30 (1975), no. 2, 207–216. http://dx.doi.org/10.1007/BF01425510 Google Scholar
[8] Davidovic, Ju. S., Korenbljum, B. I., and Hacet, B. I., A certain property of logarithmically concavefunctions. Soviet Math. Dokl. 10 (1969), 447–480; translation from Dokl. Akad. Nauk SSSR 185 (1969), 1215–1218.Google Scholar
[9] Gordon, Y., Some inequalities for Gaussian processes and applications. Israel J. Math. 50 (1985), no. 4, 265–289. http://dx.doi.org/10.1007/BF02759761 Google Scholar
[10] Kwapień, S. , A remark on the median and the expectation of convex functions of Gaussian vectors. In: Probability in Banach spaces, 9 (Sandjberg, 1993), Progr. Probab., 35, Birkhäuser Boston, Boston, MA, 1994, pp. 271–272.Google Scholar
[11] Kwapień, S., Latała, R., and Oleszkiewicz, K., Comparison of moments of sums of independent randomvariables and differential inequalities. J. Funct. Anal. 136 (1996), no. 1, 258–268. http://dx.doi.org/10.1006/jfan.1996.0030 Google Scholar
[12] Lifshits, M. A., Gaussian random functions. Mathematics and its Applications, 322, Kluwer Academic Publishers, Dordrecht, 1995.Google Scholar
[13] Litvak, A. E., Milman, V. D., and Schechtman, G., Averages of norms and quasi-norms. Math. Ann. 312 (1998), no. 1, 95–124. http://dx.doi.org/10.1007/s002080050213 Google Scholar
[14] Paouris, G., Concentration of mass on convex bodies. Geom. Funct. Anal. 16 (2006), no. 5, 1021–1049. http://dx.doi.org/10.1007/s00039-006-0584-5 Google Scholar
[15] Sudakov, V. N. and Cirel’son, B. S., Extremal properties of half-spaces for spherically invariantmeasures. J. Sov. Math. 9 (1978), 9–18; translation from Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov (LOMI) 41 (1974), 14–24, 165.Google Scholar