Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-05T02:37:04.959Z Has data issue: false hasContentIssue false
  • English
  • Français

The Shifted Classical Circulant and Skew Circulant Splitting Iterative Methods for Toeplitz Matrices

Published online by Cambridge University Press:  20 November 2018

Zhongyun Liu ,
Xiaorong Qin ,
Nianci Wu  and
Yulin Zhang
Zhongyun Liu
Affiliation:
School of Mathematics and Statistics, Changsha University of Science and Technology, Changsha 410076, P.R. China e-mail: [email protected]
Xiaorong Qin
Affiliation:
Centro de Matemática, Universidade do Minho, 4710-057 Braga, Portugal e-mail: [email protected]@[email protected]
Nianci Wu
Affiliation:
Centro de Matemática, Universidade do Minho, 4710-057 Braga, Portugal e-mail: [email protected]@[email protected]
Yulin Zhang
Affiliation:
Centro de Matemática, Universidade do Minho, 4710-057 Braga, Portugal e-mail: [email protected]@[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

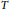It is known that every Toeplitz matrix $T$ enjoys a circulant and skew circulant splitting (denoted $\text{CSCS}$) i.e., 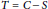$T=C-S$ a circulant matrix and $S$ a skew circulant matrix. Based on the variant of such a splitting (also referred to as $\text{CSCS}$), we first develop classical $\text{CSCS}$ iterative methods and then introduce shifted $\text{CSCS}$ iterative methods for solving hermitian positive definite Toeplitz systems in this paper. The convergence of each method is analyzed. Numerical experiments show that the classical $\text{CSCS}$ iterative methods work slightly better than the Gauss–Seidel 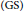$(\text{GS})$ iterative methods if the $\text{CSCS}$ is convergent, and that there is always a constant $\alpha $ such that the shifted $\text{CSCS}$ iteration converges much faster than the Gauss–Seidel iteration, no matter whether the $\text{CSCS}$ itself is convergent or not.

Keywords

15A2365F1065F15Hermitian positive definiteCSCS splittingGauss-Seidel splittingiterative methodToeplitz matrix
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 4 , 01 December 2017 , pp. 807 - 815
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Ammar, G. and W. Gragg, Superfast solution of real positive definite Toeplitz systems. SIAM J. Matrix Anal. Appl. 9(1988), 61–76. http://dx.doi.org/10.1137/0609005 Google Scholar
[2] Bai, Z.-Z., Golub, G. H., and Ng, M. K., Hermitian and skew-hermitian splitting methods for non-hermitian positive definite linear systems. SIAM J. Matrix Anal. Appl. 24(2003), no. 3, 603–626. http://dx.doi.org/10.11 37/S0895479801395458 Google Scholar
[3] Bai, Z.-Z., Golub, G. H., L.-Z. Lu, and J.-R Yin, Block triangular and skew-hermitian splitting methods for nonhermitian positive definite systems. SIAM J. Sci. Comput. 26(2005), no.3, 844–863. http://dx.doi.org/10.1137/S1064827503428114 Google Scholar
[4] Bai, Z.-Z., Golub, G. H., and J.-Y. Pan, Preconditioned hermitian and skew-hermitian splitting methods for non-hermitian positive semidefinite linear systems. Numer. Math. 98(2004), 1–32. http://dx.doi.org/10.1007/s00211-004-0521-1 Google Scholar
[5] Benzi, M., A generalization of the hermitian and skew-hermitian splitting iteration. SIAM J. Matrix Anal. Appl. 31(2009), no. 2, 360–374. http://dx.doi.org/10.1137/0807231 81 Google Scholar
[6] Benzi, M. and D. Bertaccini, Block preconditioning of real-valued iterative algorithms for complex linear systems. IMA J. Numer. Anal. 28(2008), 598–618. http://dx.doi.org/10.1093/imanum/drm039 Google Scholar
[7] Chan, R. H. and Ng, M. K., Conjugate gradient methods for Toeplitz systems. SIAM Rev. 38(1996), 427–482. http://dx.doi.org/10.1137/S0036144594276474 Google Scholar
[8] Chan, R. H. and X.-Q. Jin, Circulant and skew-circulant preconditioned for skew-hermitian type Toeplitz systems. BIT 31(1991), 632–646. http://dx.doi.org/10.1007/BF01933178 Google Scholar
[9] Commges, D. and M. Monsion, Fast inversion of triangular Toeplitz matrices. IEEE Trans. Automat. Control 29(1984), 250–251. http://dx.doi.org/10.1109/TAC.1 984.1103499 Google Scholar
[10] Frommer, A. and D.B. Szyld, H-splitting and two-stage iterative methods. Numer. Math. 63(1992), 345–356. http://dx.doi.org/10.1007/BF01385865 Google Scholar
[11] Golub, G. and C. Van Loan, Matrix computations. Third ed., Johns Hopkins Studies in the Mathematical Sciences, Johns Hopkins University Press, Baltimore, MD, 1996. Google Scholar
[12] Horn, R. A. and Johnson, C. R., Matrix analysis. Cambridge University Press, Cambridge, 1985. http://dx.doi.org/1 0.101 7/CBO9780511 81081 7 Google Scholar
[13] Lanzkron, P. J., Rose, D. J., and Syzld, D. B., Convergence of nested classical iterative methods for linear systems. Numer. Math. 58(1991), 685–702. http://dx.doi.org/10.1007/BF01385649 Google Scholar
[14] Lin, R-R., W.-K. Ching, and Ng, M. K., Fast inversion of triangular Toeplitz matrices. Theoret. Comput. Sci. 315(2004), 511–523. http://dx.doi.org/10.101 6/j.tcs.2004.01.005 Google Scholar
[15] Liu, Z. Y., Wu, H. B., and L. Lin, The two-stage iterative methods for symmetric positive definite matrices. Appl. Math. Comput. 114(2000), 1–12. http://dx.doi.org/10.1016/S0377-0427(99)00284-8 Google Scholar
[16] Nabben, R., A note on comparison theorems for splittings and multisplittings of hermitian positive definite matrices. Linear Algebra Appl. 233(1996), 67–80. http://dx.doi.org/1 0.101 6/0024-3795(94)00050-6 Google Scholar
[17] Ng, M. K., Circulant and skew-circulant splitting methods for Toeplitz systems. J. Comput. Appl. Math. 159(2003), 101–108. http://dx.doi.org/10.101 6/S0377-0427(03)00562-4 Google Scholar
[18] Ortega, J. M., Numerical analysis: A second course. Academic Press, New York, 1972. Google Scholar
[19] Saad, Y., Iterative methods for sparse Linear systems. Secon ed., SIAM, Philadelphia, PA, 2000.Google Scholar