Hostname: page-component-f554764f5-sl7kg Total loading time: 0 Render date: 2025-04-08T22:34:00.486Z Has data issue: false hasContentIssue false
  • English
  • Français

Sharpness Results and Knapp’s Homogeneity Argument

Published online by Cambridge University Press:  20 November 2018

Alex Iosevich  and
Guozhen Lu
Alex Iosevich
Affiliation:
Department of Mathematics Georgetown University Washington, DC 20057 USA, email: [email protected]
Guozhen Lu
Affiliation:
Department of Mathematics Wright State University Dayton, OH 45435 USA, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that the 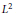${{L}^{2}}$ restriction theorem, and 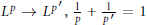${{L}^{p}}\,\to \,{{L}^{{{p}'}}}\,,\,\frac{1}{p}\,+\,\frac{1}{{{p}'}}\,=\,1$, boundedness of the surface averages imply certain geometric restrictions on the underlying hypersurface. We deduce that these bounds imply that a certain number of principal curvatures do not vanish.

Keywords

42B99
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 1 , 01 March 2000 , pp. 63 - 68
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Christ, M., Restriction of the Fourier transform to submanifolds of low codimension. Ph.D thesis, University of Chicago, 1982.Google Scholar
[2] Greenleaf, A., Principal curvature and harmonic analysis. Indiana Univ.Math. J. 30 (1981), 519–537.Google Scholar
[3] Iosevich, A. and Sawyer, E., Oscillatory integrals and maximal averages over homogeneous surfaces. Duke Math. J. 82 (1996), 103–141.Google Scholar
[4] Stein, E. M., Harmonic Analysis. Princeton Univ. Press, 1993.Google Scholar
[5] Strichartz, R., Convolutions with kernels having singularities on the sphere. Trans. Amer. Math. Soc. 148 (1970), 461–471.Google Scholar
[6] Tomas, P., A restriction theorem for the Fourier transform. Bull. Amer.Math. Soc. 81 (1975), 477–478.Google Scholar