Published online by Cambridge University Press: 20 December 2019
We obtain sharp 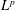 $L^{p}$ bounds for oscillatory integral operators with generic homogeneous polynomial phases in several variables. The phases considered in this paper satisfy the rank one condition that is an important notion introduced by Greenleaf, Pramanik, and Tang. Under certain additional assumptions, we can establish sharp damping estimates with critical exponents to prove endpoint
$L^{p}$ bounds for oscillatory integral operators with generic homogeneous polynomial phases in several variables. The phases considered in this paper satisfy the rank one condition that is an important notion introduced by Greenleaf, Pramanik, and Tang. Under certain additional assumptions, we can establish sharp damping estimates with critical exponents to prove endpoint 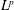 $L^{p}$ estimates.
$L^{p}$ estimates.
Danqing He was supported by NNSF of China (No. 11701583). Zuoshunhua Shi was supported in part by NNSF of China under Grant No. 11701573.