Garrison [3], Forman [2], and Abel and Siebert [1] showed that for all positive integers 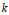$k$ and 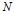$N$, there exists a positive integer 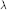$\lambda $ such that 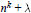${{n}^{k}}\,+\,\lambda $ is prime for at least 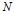$N$ positive integers 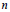$n$. In other words, there exists 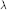$\lambda $ such that 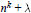${{n}^{k}}\,+\,\lambda $, represents at least 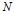$N$ primes.

We give a quantitative version of this result.We show that there exists 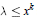$\lambda \le {{x}^{k}}$ such that 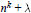${{n}^{k}}\,+\,\lambda $, 1 ≤ n ≤ x, represents at least 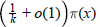$\left( \frac{1}{k}\,+\,o\left( 1 \right) \right)\,\pi \left( x \right)$ primes, as 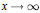$x\to \infty $. We also give some related results.