Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-05T22:25:32.387Z Has data issue: false hasContentIssue false
  • English
  • Français

Separation of Variables for

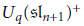
Published online by Cambridge University Press:  20 November 2018

Samuel A. Lopes
Samuel A. Lopes*
Affiliation:
Centro de Matemática da Universidade do Porto, Rua do Campo Alegre, 687, 4169-007 Porto, Portugal e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 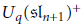${{U}_{q}}{{\left( \mathfrak{s}{{\Iota }_{n+1}} \right)}^{+}}$ be the positive part of the quantized enveloping algebra 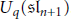${{U}_{q}}\left( \mathfrak{s}{{\Iota }_{n+1}} \right)$. Using results of Alev–Dumas and Caldero related to the center of 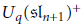${{U}_{q}}{{\left( \mathfrak{s}{{\Iota }_{n+1}} \right)}^{+}}$, we show that this algebra is free over its center. This is reminiscent of Kostant's separation of variables for the enveloping algebra 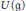$U\left( \mathfrak{g} \right)$ of a complex semisimple Lie algebra g, and also of an analogous result of Joseph–Letzter for the quantum algebra 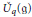${{\overset{\scriptscriptstyle\smile}{U}}_{q}}\left( \mathfrak{g} \right)$. Of greater importance to its representation theory is the fact that 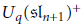${{U}_{q}}{{\left( \mathfrak{s}{{\Iota }_{n+1}} \right)}^{+}}$ is free over a larger polynomial subalgebra 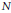$N$ in $n$ variables. Induction from 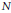$N$ to 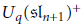${{U}_{q}}{{\left( \mathfrak{s}{{\Iota }_{n+1}} \right)}^{+}}$ provides infinite-dimensional modules with good properties, including a grading that is inherited by submodules.

Keywords

17B3716W3517B1016D60
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 4 , 01 December 2005 , pp. 587 - 600
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Alev, J. and Dumas, F., Sur le corps des fractions de certaines algèbres quantiques. J. Algebra 170(1994), 229–265.Google Scholar
[2] Benkart, G. and Gorelik, M., The separation and annihilation theorems for down-up algebras, preprint.Google Scholar
[3] Benkart, G. and Roby, T., Down-up algebras. J. Algebra 209(1998), 305–344.Google Scholar
[4] Caldero, P., Générateurs du centre de Ŭq(sl(N + 1)). Bull. Sci. Math. 118(1994), 177–208.Google Scholar
[5] Caldero, P., Sur le centre de Uq(n+). Beiträge Algebra Geom. 35(1994), 13–24,Google Scholar
[6] Caldero, P., Étude des q-commutations dans l’algèbre Uq(n+). J. Algebra 178(1995), 444–457.Google Scholar
[7] Caldero, P., On harmonic elements for semi-simple Lie algebras. Adv. Math. 166(2002), 73–99.Google Scholar
[8] De Concini, C. and Kac, V. G., Representations of quantum groups at roots of 1. In: Operator Algebras, Unitary Representations, Enveloping Algebras, and Invariant Theory, Progr. Math. 92, Birkhäuser Boston, Boston, MA, 1990, pp. 471–506.Google Scholar
[9] Dixmier, J., Sur les représentations unitaires des groupes de Lie nilpotents. IV. Canad. J. Math. 11(1959), 321–344.Google Scholar
[10] Drinfel’d, V. G., Hopf algebras and the quantum Yang-Baxter equation. Dokl. Akad. Nauk SSSR 283(1985), 1060–1064.Google Scholar
[11] Futorny, V. and Ovsienko, S., Kostant's theorem for special filtered algebras. Bull. London Math. Soc. 37(2005), 187–199.Google Scholar
[12] Jantzen, J. C., Lectures on Quantum Groups. Graduate Studies in Mathematics 6, American Mathematical Society, Providence, RI, 1996.Google Scholar
[13] Jimbo, M., A q-difference analogue of U(g) and the Yang-Baxter equation. Lett. Math. Phys. 10(1985), 63–69.Google Scholar
[14] Joseph, A. and Letzter, G., Separation of variables for quantized enveloping algebras. Amer. J. Math. 116(1994), 127–177.Google Scholar
[15] Kostant, B., Lie group representations on polynomial rings. Amer. J. Math. 85(1963), 327–404.Google Scholar
[16] Lusztig, G., Finite-dimensional Hopf algebras arising from quantized universal enveloping algebra. J. Amer.Math. Soc. 3(1990), 257–296.Google Scholar
[17] Ringel, C. M., PBW-bases of quantum groups. J. Reine Angew.Math. 470(1996), 51–88.Google Scholar
[18] Takeuchi, M., The q-bracket product and quantum enveloping algebras of classical types. J. Math. Soc. Japan 42(1990), 605–629.Google Scholar
[19] Yamane, H., A Poincaré-Birkhoff-Witt theorem for quantized universal enveloping algebras of type AN. Publ. Res. Inst.Math. Sci. 25(1989), 503–520.Google Scholar