Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T10:01:25.617Z Has data issue: false hasContentIssue false
  • English
  • Français

The Schwarz Lemma at the Boundary of the Egg Domain Bp1,p2 in ℂn

Published online by Cambridge University Press:  20 November 2018

Xiaomin Tang  and
Taishun Liu
Xiaomin Tang
Affiliation:
Department of Mathematics, Huzhou University, Huzhou, Zhejiang hËh§§§, P.R. China. e-mail: [email protected] e-mail: [email protected]
Taishun Liu
Affiliation:
Department of Mathematics, Huzhou University, Huzhou, Zhejiang hËh§§§, P.R. China. e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 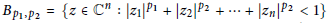${{B}_{p1,p2}}\,=\,\left\{ z\,\in \,{{\mathbb{C}}^{n}}\,:\,{{\left| {{z}_{1}} \right|}^{{{p}_{1}}}}\,+\,{{\left| {{z}_{2}} \right|}^{{{p}_{2}}}}\,+\,\cdots \,+\,{{\left| {{z}_{n}} \right|}^{{{p}_{2}}}}\,<\,1 \right\}$ be an egg domain in 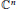${{\mathbb{C}}^{n}}$. In this paper, we first characterize the Kobayashi metric on 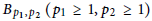${{B}_{{{p}_{1}},{{p}_{2}}}}\,\left( {{p}_{1}}\,\ge 1,\,{{p}_{2}}\,>\,1 \right)$ and then establish a new type of classical boundary Schwarz lemma at 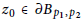${{z}_{0}}\in \partial {{B}_{{{p}_{1}},{{p}_{2}}}}$ for holomorphic self-mappings of 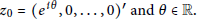${{B}_{{{p}_{1}},{{p}_{2}}}}\,\left( {{p}_{1}}\,\ge \,1,\,{{p}_{2}}\,>\,1 \right)$), where 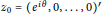${{z}_{0}}={{\left( {{e}^{i\theta }},\,0,\ldots ,0 \right)}^{\prime }}$ and 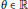$\theta \,\in \,\mathbb{R}$.

Keywords

32H0230C8032A30holomorphic mappingSchwarz lemmaKobayashi metricegg domain
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 2 , 01 June 2015 , pp. 381 - 392
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Ahlfors, L. V., An extension ofSchwarz's lemma. Trans. Amer. Math. Soc. 43 (1938), no. 3, 359–364.Google Scholar
[2] Burns, D. M. and Krantz, S. G., Rigidity of holomorphic mappings and a new Schwarz lemma at the boundary. J. Amer. Math. Soc. 7 (1994), no. 3, 661–676. http://dx.doi.org/10.1090/S0894-0347-1994-1242454-2 Google Scholar
[3] Chelst, D., A generalized Schwarz lemma at the boundary. Proc. Amer. Math. Soc. 129 (2001), no. 11, 3275–3278. http://dx.doi.org/10.1090/S0002–9939-01-06144-5 Google Scholar
[4] Franzoni, T. and Vesentini, E., Holomorphic maps and invariant distances. Notas de Matematica, 69, North-Holland, Amsterdam-New York, 1980.Google Scholar
[5] Garnett, J. B., Bounded analytic functions. Pure and Applied Mathematics, 96, Academic Press, New York, 1981.Google Scholar
[6] Huang, X., A preservation principle of extremal mappings near a strongly pseudoconvex point and its applications. Illinois J. Math. 38 (1994), no. 2, 283–302.Google Scholar
[7] Huang, X., Some applications of Bell's theorem to weakly pseudoconvex domains. Pacific J. Math. 158 (1993), no. 2, 305–315. http://dx.doi.org/10.2140/pjm.1993.158.305 Google Scholar
[8] Huang, X., A boundary rigidity problem for holomorphic mappings on some weakly pseudoconvex domains. Canad. J.Math. 47 (1995), no. 2, 405–420. http://dx.doi.org/10.4153/CJM-1995–022-3 Google Scholar
[9] Kim, K. and Lee, H., Schwarz's lemma from a differential geometric viewpoint.llSc Lecture Series, 2, IISc Press, Bangalore; World Scientific, Hackensack, NJ, 2011.Google Scholar
[10] Krantz, S. G., The Schwarz lemma at the boundary. Complex Var. Elliptic Equ. 56 (2011), no. 5, 455–468. http://dx.doi.org/10.1080/17476931003728438 Google Scholar
[11] Lelong, P., Fonction de Green pluricomplexe et lemmes de Schwarz dans les espaces de Banach. J. Math. Pures Appl. 68 (1989), no. 3, 319–347.Google Scholar
[12] Liu, T., Wang, J., and Tang, X., Schwarz lemma at the boundary of the unit ball in C” and its applications. J. Geom. Anal., 2014. http://dx.doi.Org/10.1007/s12220-014-9497-y Google Scholar
[13] Ornek, B. N., Sharpened forms of the Schwarz lemma on the boundary. Bull. Korean Math. Soc. 50 (2013), no. 6, 2053–2059. http://dx.doi.Org/10.4134/BKMS.2013.50.6.2053 Google Scholar
[14] Osserman, R., A sharp Schwarz inequality on the boundary. Proc. Amer. Math. Soc. 128 (2000), no. 12,3513–3517. http://dx.doi.org/10.1090/S0002-9939-00-05463-0 Google Scholar
[15] Rodin, B., Schwarz's lemma for circle packings. Invent. Math. 89 (1987), no. 2, 271–289. http://dx.doi.Org/10.1007/BF01389079 Google Scholar
[16] Siu, Y.-T. and Yeung, S.-K., Defects for ample divisors ofabelian varieties, Schwarz lemma, and hyperbolic hypersurfaces of low degrees. Amer. J. Math. 119 (1997), no. 5,1139–1172. http://dx.doi.Org/1 0.1353/ajm.1 997.0033 Google Scholar
[17] Taylor, A. E. and Lay, D. C., Intruduction to functional analysis. Second éd., John Wiley & Sons, New York, 1980.Google Scholar
[18] Wu, H., Normal families of holomorphic mappings. Acta Math. 119 (1967), 193–233. http://dx.doi.org/10.1007/BF02392083 Google Scholar
[19] Xiao, J. and Zhu, K., Volume integral means of holomorphic functions. Proc. Amer. Math. Soc. 139 (2011), no. 4, 1455–1465. http://dx.doi.org/10.1090/S0002–9939-2010-10797-9 Google Scholar