Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T12:48:22.949Z Has data issue: false hasContentIssue false
  • English
  • Français

Right and Left Orthogonality

Published online by Cambridge University Press:  20 November 2018

Jonathan Wild
Jonathan Wild*
Affiliation:
Collins Bay, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let V be a vector space over an arbitrary field F. In V a bilinear form

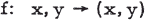
is given. If f is symmetric [(x, y) ≡ (y, x)] or skew-symmetric [(x, y) + (y, x) ≡ 0], then

1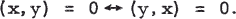

Thus right and left orthogonality coincide. It is well known that (1) implies conversely that f is either symmetric or skew-symmetric in V. We wish to give a simple proof of this result.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 4 , Issue 2 , May 1961 , pp. 182 - 184
Copyright
Copyright © Canadian Mathematical Society 1961