Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T12:54:20.174Z Has data issue: false hasContentIssue false
  • English
  • Français

The Reversibility of a Differentiable Mapping

Published online by Cambridge University Press:  20 November 2018

F. V. Atkinson
F. V. Atkinson*
Affiliation:
University of Toronto
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given n functions of n variables, in the real domain, by the equations

1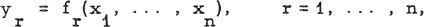

we have in various contexts to consider whether the equations are soluble for the xr when the yr are given. Such questions receive fairly complete answers in complex variable theory; a complex variable relation w = f(z) is of course brought under the heading of the real equations (1) by setting w = y1 + iy2, z = x1 + ix2. For example, if f(z) is a polynomial the fundamental theorem of algebra asserts that the equations are soluble, though not in general uniquely. Again, a basic theorem on conformal mapping gives conditions under which the equations are uniquely soluble, to the effect that a (1,1) mapping of the boundaries of domain and range implies a (1,1) mapping of the interiors.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 4 , Issue 2 , May 1961 , pp. 161 - 181
Copyright
Copyright © Canadian Mathematical Society 1961

References

1. Chaundy, T. W., Differential Calculus, (Oxford, 1935).Google Scholar
2. Haupt, O., Aumann, G., and Pauc, C. Y., Differential und Integral re chnung, Vol. II, (Berlin, 1950)Google Scholar
3. Reichbach, M., Some theorems on mappings onto, Pac. J. of Math. 10 (1960), 1397-1407.Google Scholar
4. Young, G. S., Extensions of Liouville' s theorem to n dimensions, Math. Scand. 6 (1958), 289-292.Google Scholar
5. Mac Shane, E.J and Botts, T. A., Real Analysis, (Princeton, 1959).Google Scholar
6. Seifert, H. and Threlfall, W., Topologie, (Leipzig, 1934).Google Scholar
7. Behnke, H. and Sommer, F., Analytische Funktionen, (Berlin, 1955 ).Google Scholar
8. Nagumo, M., A theory of degree of mapping based on infinitesimal analysis, Amer. J. Math. 73 (1951), 485-496.10.2307/2372303Google Scholar
9. Rodnyanskii, A.M., On differentiable mappings of regions, Doklady Akad. Nauk SSSR (N. S. ) 72 (1950), 15-17.Google Scholar
10. de la Vallée Poussin, Ch. - J., Cours d' Analyse Infinitésimale, Vol. I, (7th edition, Paris, 1930).Google Scholar
11. Carathéodory, C. and Rademacher, H., Über die Eineindeutigkeit im Kleinen und im Gros sen stetiger Abbildungen von Gebieten, Arch, der Math. u. Phys. (3), 26 (1917), 1-9.Google Scholar
12. Jacobsthal, E., Über die eineindeutige Abbildungen zweier Bereiche aufeinander bei nichtverschwindender Funktionaldéterminante, Kong. Norsk. Vidensk. Selskab Forhandlinger, 13, no. 30 (1940), 123-126.Google Scholar
13. Graves, L. M., Theory of functions of real variables, (New York, 1946).Google Scholar
14. Edelstein, M., An extension of Banach' s contraction principle, Proc. Amer. Math. Soc. 12 (1961), 7-10.Google Scholar
15. Morse, M., Calculus of Variations in the Large, (New York, 1934).10.1090/coll/018Google Scholar