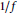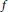Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cheng, Raymond
and
Dragas, James G.
2019.
On the failure of canonical factorization in ℓAp.
Journal of Mathematical Analysis and Applications,
Vol. 479,
Issue. 2,
p.
1939.
Cheng, Raymond
Mashreghi, Javad
and
Ross, William T.
2019.
Analysis of Operators on Function Spaces.
p.
167.
Cheng, Raymond
2019.
The zero sets of ℓAp are nested.
Illinois Journal of Mathematics,
Vol. 63,
Issue. 4,
Bénéteau, Catherine
Fleeman, Matthew
Khavinson, Dmitry
and
Sola, Alan A.
2019.
On the concept of inner function in Hardy and Bergman spaces in multiply connected domains.
Analysis and Mathematical Physics,
Vol. 9,
Issue. 2,
p.
839.
Cheng, Raymond
and
Dragas, James
2019.
A Blaschke sequence that is not a zero set for ℓ^{𝑝}_{𝐴}.
Proceedings of the American Mathematical Society,
Vol. 147,
Issue. 9,
p.
3927.
Cobos, A.
and
Seco, D.
2020.
No Entire Inner Functions.
Analysis Mathematica,
Vol. 46,
Issue. 1,
p.
39.
Bénéteau, Catherine
Ivrii, Oleg
Manolaki, Myrto
and
Seco, Daniel
2020.
Simultaneous zero-free approximation and universal optimal polynomial approximants.
Journal of Approximation Theory,
Vol. 256,
Issue. ,
p.
105389.
Le, Trieu
2020.
Inner functions in weighted Hardy spaces.
Analysis and Mathematical Physics,
Vol. 10,
Issue. 2,
Bénéteau, Catherine
Manolaki, Myrto
and
Seco, Daniel
2021.
Boundary Behavior of Optimal Polynomial Approximants.
Constructive Approximation,
Vol. 54,
Issue. 1,
p.
157.
Bénéteau, Catherine
and
Centner, Raymond
2021.
A survey of optimal polynomial approximants, applications to digital filter design, and related open problems.
Complex Analysis and its Synergies,
Vol. 7,
Issue. 2,
Abadias, Luciano
Bello, Glenier
and
Yakubovich, Dmitry
2021.
Operator inequalities, functional models and ergodicity.
Journal of Mathematical Analysis and Applications,
Vol. 498,
Issue. 2,
p.
124984.
Felder, Christopher
and
Cheng, Raymond
2022.
On the geometry of the multiplier space of ℓp
A
.
Concrete Operators,
Vol. 9,
Issue. 1,
p.
41.
Sargent, Meredith
and
Sola, Alan A.
2022.
Optimal approximants and orthogonal polynomials in several variables.
Canadian Journal of Mathematics,
Vol. 74,
Issue. 2,
p.
428.
Felder, Christopher
and
Le, Trieu
2022.
Analogues of finite Blaschke products as inner functions.
Bulletin of the London Mathematical Society,
Vol. 54,
Issue. 4,
p.
1197.
Cheng, Raymond
Ross, William T.
and
Seco, Daniel
2022.
Zeros of optimal polynomial approximants in ℓAp.
Advances in Mathematics,
Vol. 404,
Issue. ,
p.
108396.
Cheng, Raymond
and
Felder, Christopher
2023.
More properties of optimal polynomial approximants in Hardy spaces.
Pacific Journal of Mathematics,
Vol. 327,
Issue. 2,
p.
267.
Rosenfeld, Joel A.
and
Kamalapurkar, Rushikesh
2023.
Singular Dynamic Mode Decomposition.
SIAM Journal on Applied Dynamical Systems,
Vol. 22,
Issue. 3,
p.
2357.
Rosenfeld, Joel A.
and
Kamalapurkar, Rushikesh
2023.
Convergent Dynamic Mode Decomposition.
p.
4972.
Cheng, Raymond
and
Felder, Christopher
2024.
Recent Progress in Function Theory and Operator Theory.
Vol. 799,
Issue. ,
p.
107.