Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T09:09:51.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarks on a Problem of Moser

Published online by Cambridge University Press:  20 November 2018

V. Chvátal
V. Chvátal*
Affiliation:
Stanford University, Stanford, California
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M(n) be the set of all the points (x1, x2,…, xn)∈En such that xi∈{0,1,2} for each i= 1, 2,…, n and let f(n) be the cardinality of a largest subset of M(n) containing no three distinct collinear points. L. moser [4] asked for a proof of the inequality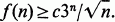

Let us consider the set Sn of those points (x1x2,…, xn)∈M(n) which satisfy |{i:Xi= 1}| = [(n +1)/3]. As Sn is a subset of the sphere with center at (1, 1,…, 1) and radius (n-[(n+1)/3])1/2, no three distinct points of Sn are collinear. Thus we have

1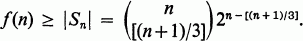

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 15 , Issue 1 , March 1972 , pp. 19 - 21
Copyright
Copyright © Canadian Mathematical Society 1972

References

References

1. V. Chvátal, Some unknown Van der Waerden numbers, Combinatorial structures and their applications (Guy, R. K. et al., ed.), Gordon and Breach, New York (1970), 31-33.Google Scholar
2. Hales, A. W. and Jewett, R. I., Regularity and positional games, Trans. Amer. Math. Soc. 106 (1963), 222-229.Google Scholar
3. Moser, L., Problem 21, Proc. of Number Theory Conference, Univ. of Colorado, 1963, Mimeographed, 79.Google Scholar
4. Moser, L., Problem P. 170, Canad. Math. Bull. 13 (1970), p. 268.Google Scholar
5. Roth, K. F., On certain sets of integers, J. Londo. Math. Soc. 28 (1953), 104-109.Google Scholar
6. Szemerédi, E., On sets of integers containing no four elements in arithmetic progression, Acta. Math. Acad. Sci. Hungar. 20 (1969), 89-104.Google Scholar
7. Van der Waerden, B. L., Beweis einer Baudetschen Vermutung, Nieuw Arch. Wisk. 15 (1928), 212-216.Google Scholar

References

1. V. Chvátal, Some unknown Van der Waerden numbers, Combinatorial structures and their applications (Guy, R. K. et al., ed.), Gordon and Breach, New York (1970), 31-33.Google Scholar
2. Hales, A. W. and Jewett, R. I., Regularity and positional games, Trans. Amer. Math. Soc. 106 (1963), 222-229.Google Scholar
3. Moser, L., Problem 21, Proc. of Number Theory Conference, Univ. of Colorado, 1963, Mimeographed, 79.Google Scholar
4. Moser, L., Problem P. 170, Canad. Math. Bull. 13 (1970), p. 268.Google Scholar
5. Roth, K. F., On certain sets of integers, J. Londo. Math. Soc. 28 (1953), 104-109.Google Scholar
6. Szemerédi, E., On sets of integers containing no four elements in arithmetic progression, Acta. Math. Acad. Sci. Hungar. 20 (1969), 89-104.Google Scholar
7. Van der Waerden, B. L., Beweis einer Baudetschen Vermutung, Nieuw Arch. Wisk. 15 (1928), 212-216.Google Scholar