Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T20:04:40.242Z Has data issue: false hasContentIssue false
  • English
  • Français

A Real-analytic Nonpolynomially Convex Isotropic Torus with no Attached Discs

Published online by Cambridge University Press:  20 November 2018

Purvi Gupta
Purvi Gupta*
Affiliation:
Department of Mathematics, University of Western Ontario, London, ON N6A 5B7 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We showbymeans of an example in 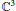${{\mathbb{C}}^{3}}$ that Gromov’s theoremon the presence of attached holomorphic discs for compact Lagrangianmanifolds is not true in the subcritical real-analytic case, even in the absence of an obvious obstruction, i.e., polynomial convexity.

Keywords

32V4032E2053D12polynomial hullisotropic submanifoldholomorphic disc
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 2 , 01 June 2018 , pp. 289 - 291
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Alexander, H., Disks with boundaries in totally real and Lagrangian manifolds. Duke Math. J. 100(1999), no. 1, 131–138.http://dx.doi.org/10.1215/S0012-7094-99-10004-4 Google Scholar
[2] Duval, J., Convexite rationnelle des surfaces lagrangiennes. Invent. Math. 104(1991), no. 3, 581–599.http://dx.doi.Org/10.1007/BF01245091 Google Scholar
[3] Duval, J. and Gayet, D., Riemann surfaces and totally real tori. Comment. Math. Helv. 89(2014), 299–312. http://dx.doi.org/10.4171/CMH/320 Google Scholar
[4] Duval, J. and Sibony, N., Polynomial convexity, rational convexity, and currents. Duke Math. J. 79(1995), no. 2, 487–513.http://dx.doi.org/10.1215/S0012-7094-95-07912-5 Google Scholar
[5] Gromov, M., Pseudo-holomorphic curves in symplectic manifolds. Invent. Math. 82(1985), no. 2, 307–347.http://dx.doi.Org/10.1007/BF01388806 Google Scholar
[6] Izzo, A. J., H. Kalm, S., and Wold, E. F., Presence or absence ofanalytic strueture in maximal ideal Spaces. Math. Ann. 366(2016), no. 1-2, 459–478.http://dx.doi.org/10.1007/s00208-01 5-1330-9 Google Scholar
[7] Jimbo, T., Polynomial hulls ofgraphs on the torus in . Sci. Math. Jpn. 62(2005), 335–342.Google Scholar
[8] Rudin, W., Pairs of inner funetions onfinite Riemann surfaces. Trans. Amer. Math. Soc. 140(1969), 423–434.http://dx.doi.org/10.1090/S0002-9947-1969-0241629-0 Google Scholar