A preordering $T$ is constructed in the polynomial ring 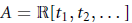$A=\mathbb{R}[{{t}_{1}},{{t}_{2}},...]$ (countablymany variables) with the following two properties: (1) For each 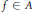$f\,\in \,A$ there exists an integer $N$ such that 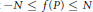$-\,N\,\le \,f\left( p \right)\,\le \,N$ holds for all 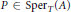$P\in \text{Spe}{{\text{r}}_{T}}(A)$. (2) For all 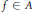$f\,\in \,A$, if 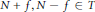$N+f,N-f\in T$ for some integer $N$, then 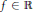$f\,\in \,\mathbb{R}$. This is in sharp contrast with the Schmüdgen-Wörmann result that for any preordering $T$ in a finitely generated $\mathbb{R}$-algebra $A$, if property (1) holds, then for any 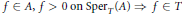$f\in A,f>0\,\text{on}\,\text{Spe}{{\text{r}}_{T}}(A)\Rightarrow f\in T$. Also, adjoining to $A$ the square roots of the generators of $T$ yields a larger ring $C$ with these same two properties but with 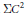$\sum{{{C}^{2}}}$ (the set of sums of squares) as the preordering.