Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Merris, Russell
1979.
Recent advances in symmetry classes of tensors†.
Linear and Multilinear Algebra,
Vol. 7,
Issue. 4,
p.
317.
Carlson, David
and
Loewy, Raphael
1980.
Induced bilinear maps and matrix equations†.
Linear and Multilinear Algebra,
Vol. 9,
Issue. 1,
p.
17.
Lim, M. H.
1992.
Conditions on decomposable symmetric tensors as an algebraic variety.
Linear and Multilinear Algebra,
Vol. 32,
Issue. 3-4,
p.
249.
Lim, M.H.
1995.
A uniqueness theorem on symmetric tensors.
Linear Algebra and its Applications,
Vol. 231,
Issue. ,
p.
153.
Dias da Silva, J.A.
and
Rodrigues, Fátima
2006.
Decomposable critical tensors.
Linear Algebra and its Applications,
Vol. 414,
Issue. 1,
p.
172.
Lim, Ming-Huat
2008.
Additive preservers of non-zero decomposable tensors.
Linear Algebra and its Applications,
Vol. 428,
Issue. 1,
p.
239.
Chooi, Wai Leong
Kwa, Kiam Heong
and
Lim, Ming-Huat
2017.
Coherence invariant maps on tensor products.
Linear Algebra and its Applications,
Vol. 516,
Issue. ,
p.
24.
Xu, Changqing
He, Lingling
and
Lin, Zerong
2020.
Commutation matrices and commutation tensors.
Linear and Multilinear Algebra,
Vol. 68,
Issue. 9,
p.
1721.
Heong Kwa, Kiam
2024.
Coherence invariant maps on order-3 symmetric tensors.
Linear and Multilinear Algebra,
Vol. 72,
Issue. 4,
p.
597.
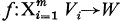 is said to be symmetric with respect to G and χ if
is said to be symmetric with respect to G and χ if