Let 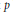$p$ be a prime number. Let 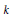$k$ be a finite field of characteristic 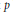$p$. The subset 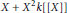$X\,+\,{{X}^{2}}k[[X]]$ of the ring 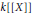$k\left[\!\left[ X \right]\!\right]$ is a group under the substitution law $\circ $ sometimes called the Nottingham group of 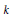$k$, it is denoted by 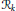${{\mathcal{R}}_{k}}$. The ramification of one series 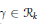$\gamma \,\in \,{{\mathcal{R}}_{k}}$ is caracterized by its lower ramification numbers: 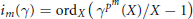${{i}_{m}}(\gamma )\,=\,\text{or}{{\text{d}}_{X}}({{\gamma }^{{{p}^{m}}}}\,(X)/X-1)\,$, as well as its upper ramification numbers:

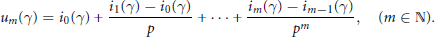$${{u}_{m}}(\gamma )\ =\ {{i}_{0}}(\gamma )+\frac{{{i}_{1}}(\gamma )-{{i}_{0}}(\gamma )}{p}\,+\,.\,.\,.\,+\,\frac{{{i}_{m}}(\gamma )-{{i}_{m-1}}(\gamma )}{{{p}^{m}}},\,\,\,\,\,\,(m\,\in \,\mathbb{N}).$$

By Sen's theorem, the 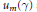${{u}_{m}}(\gamma )$ are integers. In this paper, we determine the sequences of integers (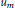${{u}_{m}}$) for which there exists 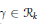$\gamma \,\in \,{{\mathcal{R}}_{k}}$ such that 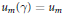${{u}_{m}}(\gamma )\,=\,{{u}_{m}}$ for all integer 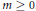$m\,\ge \,0$.