Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-15T18:16:04.903Z Has data issue: false hasContentIssue false
  • English
  • Français

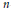Quantization of Bending Deformations of Polygons In , Hypergeometric Integrals and the Gassner Representation

Published online by Cambridge University Press:  20 November 2018

Michael Kapovich  and
John J. Millson
Michael Kapovich
Affiliation:
Department of Mathematics University of Utah Salt Lake City, Utah 84112 USA, email: [email protected]
John J. Millson
Affiliation:
Department of Mathematics University of Maryland College Park, Maryland 20742 USA, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

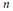The Hamiltonian potentials of the bending deformations of $n$-gons in 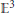${{\mathbb{E}}^{3}}$ studied in 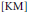$\left[ \text{KM} \right]$ and [Kly] give rise to a Hamiltonian action of the Malcev Lie algebra 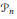${{P}_{n}}$ of the pure braid group 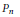${{P}_{n}}$ on the moduli space 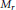${{M}_{r}}$ of 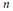$n$-gon linkages with the side-lengths 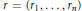$r\,=\,\left( {{r}_{1}},\ldots ,{{r}_{n}} \right)$ in 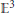${{\mathbb{E}}^{3}}$. If 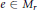$e\,\in \,{{M}_{r}}$ is a singular point we may linearize the vector fields in 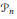${{P}_{n}}$ at $e$. This linearization yields a flat connection 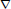$\nabla$ on the space 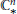$\mathbb{C}_{*}^{n}$ of 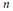$n$ distinct points on 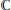$\mathbb{C}$. We show that the monodromy of $\nabla$ is the dual of a quotient of a specialized reduced Gassner representation.

Keywords

53D3053D50
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 44 , Issue 1 , 01 March 2001 , pp. 36 - 60
Copyright
Copyright © Canadian Mathematical Society 2001

References

[ABC] Amoros, J., Burger, M., Corlette, K., Kotschick, D. and Toledo, D., Fundamental groups of Kähler manifolds. Amer.Math. Soc., Mathematical Surveys and Monographs 44, 1996.Google Scholar
[Bi] Birman, J., Braids, links and mapping class groups, Ann. of Math. Studies 82, Princeton Univ. Press, 1975.Google Scholar
[C] Cartier, P., Développements récents sur les groupes de tresses. Applications à la topologie et à l’algèbre. Séminaire Bourbaki (716) 42(1989–90), 17–77.Google Scholar
[DM] Deligne, P. and Mostow, G., Monodromy of hypergeometric functions and non-lattice integral monodromy. Inst. Hautes Études Sci. Publ. Math. 63 (1986), 5–90.Google Scholar
[H] Hartshorne, R., Algebraic geometry. Springer Verlag, 1977.Google Scholar
[I] Ihara, Y., Automorphisms of pure sphere braid groups and Galois representations. Grothendieck Festschrift, Vol. II, Progress in Math., Birkhauser, 1990, 353–373.Google Scholar
[KO] Katz, N. and Oda, T., On the differentiation of de Rham cohomology classes with respect to parameters. J. Math. Kyoto Univ. 8 (1968), 199–213.Google Scholar
[K1] Kohno, T., Linear representations of braid groups and classical Yang-Baxter equations. ContemporaryMath. 78 (1988), 339–363.Google Scholar
[K2] Kohno, T., Série de Poincare-Koszul associée aux groupes de tresses pures Invent.Math. 82 (1985), 57–75.Google Scholar
[Kly] Klyachko, A., Spatial polygons and stable configurations of points on the projective line. In: Algebraic geometry and its applications Yaroslavl, 1992, 67–84.Google Scholar
[KM] Kapovich, M. and Millson, J. J., The symplectic geometry of polygons in Euclidean space. J. Differential Geometry 44 (1996), 479–513.Google Scholar
[Lo] Long, D. D., On the linear representation of the braid groups. Trans. Amer.Math. Soc. 311 (1989), 535–560.Google Scholar
[Mo] Moran, S., The mathematical theory of knots and braids. An introduction. North-Holland, Math. Studies 82, 1983.Google Scholar