Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T05:17:03.238Z Has data issue: false hasContentIssue false
  • English
  • Français

A Quantitative Estimate on Fixed-Points of Composite Meromorphic Functions

Published online by Cambridge University Press:  20 November 2018

Jian-Hua Zheng
Jian-Hua Zheng*
Affiliation:
Department of Applied Mathematics, Tsing Hua University, Beijing, 100084, People's Republic of China
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ƒ(z) be a transcendental meromorphic function of finite order, g(z) a transcendental entire function of finite lower order and let α(z) be a non-constant meromorphic function with T(r, α) = S(r,g). As an extension of the main result of [7], we prove that

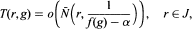
where J has a positive lower logarithmic density.

Keywords

30D0530D35
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 38 , Issue 4 , 01 December 1995 , pp. 490 - 495
Copyright
Copyright © Canadian Mathematical Society 1995

References

1. Bergweiler, W., On the composition of transcendental entire and meromorphic functions, preprint.Google Scholar
2. Bergweiler, W., Fix-points of meromorphic functions and iterated entire functions, J. Math. Anal. Appl. (1) 151 (1990), 261–274.Google Scholar
3. Bergweiler, W. and Yang, C. C., On the value distribution of composite meromorphic functions, Bull. London Math. Soc. 25(1993), 357–361.Google Scholar
4. Dai, C., D. Drasin and Li, B., On the growth of entire and meromorphic functions of infinite order, J. Analyse Math. 55(1990), 217–228.Google Scholar
5. Gross, F. and Osgood, C. F., A simpler proof of a theorem of Steinmetz, J. Math. Anal. Appl. 143(1989), 290–294.Google Scholar
6. Hayman, W. K., On the characteristic of functions meromorphic in the plane and of their integrals, Proc. London Math. Soc. (3) 14A(1965), 93–128.Google Scholar
7. Katajamàki, K., Kinnunen, L. and 1. Laine, On the value distribution of some composite meromorphic functions, Bull. London Math. Soc 25(1993), 445–452.Google Scholar
8. Langley, J., On the fixpoints of composite entire functions of finite order, Proc. Roy. Soc. Edinburgh, to appear.Google Scholar
9. Niino, K. and Suita, N., Growth of a composite function of entire functions, Kodai Math. J. (3) 3(1980), 374–379.Google Scholar
10. Steinmetz, N., Vber die faktoriserbaren Losungen gewohnliches differentialgleichungen, Math. Z. 170 (1980), 169–180.Google Scholar
11. Zheng, J. H. and Yang, C. C., Further results on fix-points and zeros of entire functions, Trans. Amer. Math. Soc. 347(1995), 37–50.Google Scholar
12. Zheng, J. H. and Yang, C. C., Estimate on the number of fix-points of composite entire functions, Complex Variables Theory Appl. 23(1993).Google Scholar