Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fanggui, Wang
1999.
wDimension of domains.
Communications in Algebra,
Vol. 27,
Issue. 5,
p.
2267.
Dumitrescu, Tiberiu
and
Zafrullah, Muhammad
2001.
LCM-splitting sets in some ring extensions.
Proceedings of the American Mathematical Society,
Vol. 130,
Issue. 6,
p.
1639.
Fanggui, Wang
2001.
w-DIMENSION OF DOMAINS. II.
Communications in Algebra,
Vol. 29,
Issue. 6,
p.
2419.
FONTANA, M.
JARA, P.
and
SANTOS, E.
2003.
PRÜFER ⋆-MULTIPLICATION DOMAINS AND SEMISTAR OPERATIONS.
Journal of Algebra and Its Applications,
Vol. 02,
Issue. 01,
p.
21.
Fontana, Marco
and
Loper, K. Alan
2003.
Nagata Rings, Kronecker Function Rings, and Related Semistar Operations.
Communications in Algebra,
Vol. 31,
Issue. 10,
p.
4775.
El Baghdadi, S.
Fontana, Marco
and
Picozza, Giampaolo
2004.
Semistar Dedekind domains.
Journal of Pure and Applied Algebra,
Vol. 193,
Issue. 1-3,
p.
27.
El Baghdadi, Said
and
Fontana, Marco
2004.
Semistar Linkedness and Flatness, Prüfer Semistar Multiplication Domains.
Communications in Algebra,
Vol. 32,
Issue. 3,
p.
1101.
Chang, Gyu Whan
and
Zafrullah, Muhammad
2006.
The w-integral closure of integral domains.
Journal of Algebra,
Vol. 295,
Issue. 1,
p.
195.
Fontana, Marco
and
Loper, K. Alan
2006.
Multiplicative Ideal Theory in Commutative Algebra.
p.
169.
Wang, Fang Gui
2006.
On t–Dimension over Strong Mori Domains.
Acta Mathematica Sinica, English Series,
Vol. 22,
Issue. 1,
p.
131.
Chang, Gyu Whan
2006.
∗-Noetherian domains and the ring D[X]N∗.
Journal of Algebra,
Vol. 297,
Issue. 1,
p.
216.
Coykendall, Jim
and
Dumitrescu, Tiberiu
2007.
Integral Domains Having Nonzero Elements with Infinitely Many Prime Divisors.
Communications in Algebra,
Vol. 35,
Issue. 4,
p.
1333.
Gabelli, Stefania
and
Picozza, Giampaolo
2007.
Star stable domains.
Journal of Pure and Applied Algebra,
Vol. 208,
Issue. 3,
p.
853.
Kabbaj, S
and
Mimouni, A
2007.
t-class semigroups of integral domains.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2007,
Issue. 612,
Chang, Gyu Whan
2008.
Prüfer ∗-multiplication domains, Nagata rings, and Kronecker function rings.
Journal of Algebra,
Vol. 319,
Issue. 1,
p.
309.
Fontana, Marco
and
Loper, K. Alan
2009.
Cancellation properties in ideal systems: A classification of e.a.b. semistar operations.
Journal of Pure and Applied Algebra,
Vol. 213,
Issue. 11,
p.
2095.
Coykendall, Jim
and
Dutta, Tridib
2010.
A Generalization of Integrality.
Canadian Mathematical Bulletin,
Vol. 53,
Issue. 4,
p.
639.
Fontana, Marco
and
Picozza, Giampaolo
2011.
On some classes of integral domains defined by Krullʼs a.b. operations.
Journal of Algebra,
Vol. 341,
Issue. 1,
p.
179.
Bazzoni, Silvana
and
Kabbaj, Salah-Eddine
2011.
Commutative Algebra.
p.
47.
Fontana, Marco
and
Zafrullah, Muhammad
2011.
Commutative Algebra.
p.
145.
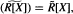 , where X is a family of indeterminates; pseudo-integrality is analyzed in rings of the form D + M; and an example is given to show that pseudo-integrality does not behave well with respect to
localization.
, where X is a family of indeterminates; pseudo-integrality is analyzed in rings of the form D + M; and an example is given to show that pseudo-integrality does not behave well with respect to
localization.

