1 Formulation of main results
1.1
Let
![]() $BV(I)$
be the space of complex-valued functions of bounded variation on the interval
$BV(I)$
be the space of complex-valued functions of bounded variation on the interval
![]() $I=[a,b]$
. By definition,
$I=[a,b]$
. By definition,
![]() $f\in BV(I)$
if and only if
$f\in BV(I)$
if and only if
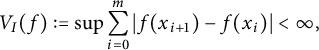 $$ \begin{align} V_I(f):=\sup \sum_{i=0}^m|f(x_{i+1})-f(x_i)|<\infty, \end{align} $$
$$ \begin{align} V_I(f):=\sup \sum_{i=0}^m|f(x_{i+1})-f(x_i)|<\infty, \end{align} $$
where the supremum is taken over all partitions
![]() $a=x_0<x_1<\cdots <x_m=b$
,
$a=x_0<x_1<\cdots <x_m=b$
,
![]() $m\in \mathbb {N}$
, of I. In this paper, we study algebraic properties of weakly inverse-closed complex Banach function algebras generated by
$m\in \mathbb {N}$
, of I. In this paper, we study algebraic properties of weakly inverse-closed complex Banach function algebras generated by
![]() $BV(I)$
functions. Here, by a complex Banach function algebra, we mean a unital subalgebra A of the algebra of complex-valued functions on a set X with pointwise sum and product equipped with a norm that makes A a Banach algebra. Such an algebra A is called weakly inverse-closed if it satisfies the condition:
$BV(I)$
functions. Here, by a complex Banach function algebra, we mean a unital subalgebra A of the algebra of complex-valued functions on a set X with pointwise sum and product equipped with a norm that makes A a Banach algebra. Such an algebra A is called weakly inverse-closed if it satisfies the condition:
-
(wi) If
 $f\in A$
, and
$f\in A$
, and
 $\sup _{X}|f(x)|<1$
, then
$\sup _{X}|f(x)|<1$
, then
 $\frac {1}{1-f}\in A$
.
$\frac {1}{1-f}\in A$
.
To formulate the results, recall that a unital commutative ring R is said to be projective free if every finitely generated projective R-module is free (i.e., if M is an R-module such that
![]() $M\oplus N\cong R^n$
for an R-module N and
$M\oplus N\cong R^n$
for an R-module N and
![]() $n \in \mathbb {Z} _+\, (:= \mathbb {N}\cup \{0\})$
, then
$n \in \mathbb {Z} _+\, (:= \mathbb {N}\cup \{0\})$
, then
![]() $M\cong R^m$
for some
$M\cong R^m$
for some
![]() $m \in \mathbb {Z} _+$
). Let
$m \in \mathbb {Z} _+$
). Let
![]() $M_n(R)$
denote the ring of
$M_n(R)$
denote the ring of
![]() $n\times n$
matrices over R and
$n\times n$
matrices over R and
![]() $GL_n(R)$
its unit group. In terms of matrices, the ring R is projective-free if and only if for each
$GL_n(R)$
its unit group. In terms of matrices, the ring R is projective-free if and only if for each
![]() $n\in \mathbb {N}$
, every
$n\in \mathbb {N}$
, every
![]() $X\in M_n(R)\setminus \{0_n, I_n\}$
such that
$X\in M_n(R)\setminus \{0_n, I_n\}$
such that
![]() $X^2=X$
(i.e., an idempotent) has a form
$X^2=X$
(i.e., an idempotent) has a form
![]() $X=S(I_r\oplus 0_{n-r})S^{-1}$
for some
$X=S(I_r\oplus 0_{n-r})S^{-1}$
for some
![]() $ S\in GL_n(R)$
,
$ S\in GL_n(R)$
,
![]() $r\in \{1,\dots , n-1\}$
; here,
$r\in \{1,\dots , n-1\}$
; here,
![]() $0_k$
and
$0_k$
and
![]() $I_k$
are zero and identity matrices in
$I_k$
are zero and identity matrices in
![]() $M_k(R)$
(see [Reference Cohn9, Proposition 2.6]). (For some examples of projective-free rings and their applications, see, e.g., [Reference Brudnyi and Sasane8, Reference Lam17, Reference Vidyasagar25] and the references therein.)
$M_k(R)$
(see [Reference Cohn9, Proposition 2.6]). (For some examples of projective-free rings and their applications, see, e.g., [Reference Brudnyi and Sasane8, Reference Lam17, Reference Vidyasagar25] and the references therein.)
Let
![]() $A\subset \ell ^{\infty }(I)$
be a weakly inverse-closed complex Banach function algebra such that the subalgebra
$A\subset \ell ^{\infty }(I)$
be a weakly inverse-closed complex Banach function algebra such that the subalgebra
![]() $A\cap BV(I)$
is dense in A. We denote by
$A\cap BV(I)$
is dense in A. We denote by
![]() $1_I$
the unit of A (i.e., the constant function of value
$1_I$
the unit of A (i.e., the constant function of value
![]() $1$
on I). For a nonzero idempotent
$1$
on I). For a nonzero idempotent
![]() $p\in A$
, we set
$p\in A$
, we set
![]() $A_p:=\{pg\, :\, g\in A\}$
. Then
$A_p:=\{pg\, :\, g\in A\}$
. Then
![]() $A_p$
is a closed subalgebra of A with unit p. If M is an A-module, then
$A_p$
is a closed subalgebra of A with unit p. If M is an A-module, then
![]() $M_p:=\{pm\, :\, m\in M\}$
is a submodule which can be regarded as an
$M_p:=\{pm\, :\, m\in M\}$
is a submodule which can be regarded as an
![]() $A_p$
-module as its annihilator contains
$A_p$
-module as its annihilator contains
![]() $\mathrm {ker}\,(1_I-p)$
.
$\mathrm {ker}\,(1_I-p)$
.
Theorem 1.1 Let M be a finitely generated projective A-module. Then there exist idempotents
![]() $p_1,\dots , p_k\in A$
such that
$p_1,\dots , p_k\in A$
such that
![]() $M=\oplus _{i=1}^k\, M_{p_i}$
and each
$M=\oplus _{i=1}^k\, M_{p_i}$
and each
![]() $M_{p_i}$
is a free
$M_{p_i}$
is a free
![]() $A_{p_i}$
-module. In particular, if
$A_{p_i}$
-module. In particular, if
![]() $A\subset C(I)$
, then it is a projective-free ring.
$A\subset C(I)$
, then it is a projective-free ring.
For instance, Theorem 1.1 holds true for weakly inverse-closed complex Banach function algebras
![]() $A\subset BV(I)$
and their uniform closures
$A\subset BV(I)$
and their uniform closures
![]() $\bar A\subset \ell ^{\infty }(I)$
.
$\bar A\subset \ell ^{\infty }(I)$
.
In terms of matrices, Theorem 1.1 asserts that for every idempotent
![]() $X\in M_n(A)$
,
$X\in M_n(A)$
,
![]() $n\in \mathbb {N}$
, there exist idempotents
$n\in \mathbb {N}$
, there exist idempotents
![]() $p_1,\dots , p_k\in A$
with
$p_1,\dots , p_k\in A$
with
![]() $\sum _{j=1}^k p_j=1$
and
$\sum _{j=1}^k p_j=1$
and
![]() $I_1,\dots , I_k\in M_n({\mathbb C})$
,
$I_1,\dots , I_k\in M_n({\mathbb C})$
,
![]() $k\in \mathbb {N}$
, and an invertible matrix
$k\in \mathbb {N}$
, and an invertible matrix
![]() $G\in GL_n(A)$
such that
$G\in GL_n(A)$
such that
![]() $G^{-1}XG=\sum _{j=1}^k p_jI_j$
(see Section 4 for an operator-valued generalization of this result).
$G^{-1}XG=\sum _{j=1}^k p_jI_j$
(see Section 4 for an operator-valued generalization of this result).
Let A be an associative ring with unit. For a natural number n, let
![]() $U_n(A)$
denote the set of unimodular elements of
$U_n(A)$
denote the set of unimodular elements of
![]() $A^n$
, i.e.,
$A^n$
, i.e.,
An element
![]() $(a_1,\dots , a_n)\in U_n(A)$
is called reducible if there exist
$(a_1,\dots , a_n)\in U_n(A)$
is called reducible if there exist
![]() $c_1,\dots , c_{n-1}\in A$
such that
$c_1,\dots , c_{n-1}\in A$
such that
![]() $(a_1+c_1 a_n,\dots , a_{n-1}+c_{n-1}a_n)\in U_{n-1}(A).$
The stable rank of A is the least n such that every element of
$(a_1+c_1 a_n,\dots , a_{n-1}+c_{n-1}a_n)\in U_{n-1}(A).$
The stable rank of A is the least n such that every element of
![]() $U_{n+1}(A)$
is reducible. The concept of the stable rank introduced by Bass [Reference Bass2] plays an important role in some stabilization problems of algebraic K-theory. Following Vaserstein [Reference Vaserstein24], we call a ring of stable rank
$U_{n+1}(A)$
is reducible. The concept of the stable rank introduced by Bass [Reference Bass2] plays an important role in some stabilization problems of algebraic K-theory. Following Vaserstein [Reference Vaserstein24], we call a ring of stable rank
![]() $1$
a B-ring. (We refer to this paper for some examples and properties of B-rings.)
$1$
a B-ring. (We refer to this paper for some examples and properties of B-rings.)
Theorem 1.2 Each weakly inverse-closed complex Banach function algebra
![]() ${A\subset BV(I)}$
is a B-ring.
${A\subset BV(I)}$
is a B-ring.
Example 1.3 Since every closed unital subalgebra of a weakly inverse-closed complex Banach function algebra is weakly inverse-closed (see Lemma 2.1), Theorems 1.1 and 1.2 are applicable to closed unital subalgebras of the following weakly inverse-closed function algebras: (a)
![]() $(BV(I),\lVert \cdot \rVert _{BV})$
, where
$(BV(I),\lVert \cdot \rVert _{BV})$
, where
![]() $\lVert f\rVert _{BV}:=\sup _{I}|f|+V_I(f)$
; (b)
$\lVert f\rVert _{BV}:=\sup _{I}|f|+V_I(f)$
; (b)
![]() $(AC(I),\lVert \cdot \rVert _{AC})$
—the algebra of absolutely continuous complex-valued functions on I, where
$(AC(I),\lVert \cdot \rVert _{AC})$
—the algebra of absolutely continuous complex-valued functions on I, where
![]() $\|f\|_{AC}:=\max _I |f|+\int _I\, |f'(t)|\,dt$
; (c)
$\|f\|_{AC}:=\max _I |f|+\int _I\, |f'(t)|\,dt$
; (c)
![]() $(\mathrm {Lip}(I),\lVert \cdot \rVert _{\mathrm {Lip}})$
—the algebra of complex-valued Lipschitz functions on I, where
$(\mathrm {Lip}(I),\lVert \cdot \rVert _{\mathrm {Lip}})$
—the algebra of complex-valued Lipschitz functions on I, where
![]() $\|f\|_{\mathrm {Lip}}:=\max _I |f|+\sup _{x\ne y}\frac {|f(x)-f(y)|}{|x-y|}$
; and (d)
$\|f\|_{\mathrm {Lip}}:=\max _I |f|+\sup _{x\ne y}\frac {|f(x)-f(y)|}{|x-y|}$
; and (d)
![]() $(C^k(I),\lVert \cdot \rVert _{C^k})$
—the algebra of complex-valued
$(C^k(I),\lVert \cdot \rVert _{C^k})$
—the algebra of complex-valued
![]() $C^k$
functions on I,
$C^k$
functions on I,
![]() $k\ge 1$
, where
$k\ge 1$
, where
![]() $\|f\|_{C^k}:=\sum _{i=0}^k \max _I |f^{(i)}|$
.
$\|f\|_{C^k}:=\sum _{i=0}^k \max _I |f^{(i)}|$
.
1.2
Theorems 1.1 and 1.2 are derived from a general result presented in this section. For its formulation, recall that for a commutative unital complex Banach algebra A, the maximal ideal space
![]() $\mathfrak M(A)\subset A^{\ast }$
is the set of nonzero homomorphisms
$\mathfrak M(A)\subset A^{\ast }$
is the set of nonzero homomorphisms
![]() $A \!\rightarrow \! {\mathbb C}$
endowed with the Gelfand topology, the weak-
$A \!\rightarrow \! {\mathbb C}$
endowed with the Gelfand topology, the weak-
![]() $\ast $
topology of
$\ast $
topology of
![]() $A^{\ast }$
. It is a compact Hausdorff space contained in the unit sphere of
$A^{\ast }$
. It is a compact Hausdorff space contained in the unit sphere of
![]() $A^{\ast }$
. The Gelfand transform defined by
$A^{\ast }$
. The Gelfand transform defined by
![]() $\hat {a}(\varphi ):=\varphi (a)$
for
$\hat {a}(\varphi ):=\varphi (a)$
for
![]() $a\in A$
and
$a\in A$
and
![]() $\varphi \in \mathfrak M(A)$
is a nonincreasing-norm morphism from A into
$\varphi \in \mathfrak M(A)$
is a nonincreasing-norm morphism from A into
![]() $C(\mathfrak M (A))$
, the Banach algebra of complex-valued continuous functions on
$C(\mathfrak M (A))$
, the Banach algebra of complex-valued continuous functions on
![]() $\mathfrak M(A)$
. Also, recall that the covering dimension of a topological space X, denoted by
$\mathfrak M(A)$
. Also, recall that the covering dimension of a topological space X, denoted by
![]() $\mathrm {dim}\, X$
, is the smallest integer d such that every open cover of X has an open refinement of order at most
$\mathrm {dim}\, X$
, is the smallest integer d such that every open cover of X has an open refinement of order at most
![]() $d+1$
. If no such integer exists, then X is said to have infinite covering dimension.
$d+1$
. If no such integer exists, then X is said to have infinite covering dimension.
Theorem 1.4 Let
![]() $A\subset \ell ^{\infty }(I)$
be a weakly inverse-closed complex Banach function algebra such that
$A\subset \ell ^{\infty }(I)$
be a weakly inverse-closed complex Banach function algebra such that
![]() $A\cap BV(I)$
is dense in A. Then
$A\cap BV(I)$
is dense in A. Then
![]() $\mathrm {dim}\,\mathfrak M(A)\le 2$
and the Čech cohomology group
$\mathrm {dim}\,\mathfrak M(A)\le 2$
and the Čech cohomology group
![]() $H^2(\mathfrak M(A),\mathbb {Z} )=0$
.
$H^2(\mathfrak M(A),\mathbb {Z} )=0$
.
Note that for a weakly inverse-closed complex Banach function algebra
![]() $A\subset \ell ^{\infty }(I)$
with uniform closure
$A\subset \ell ^{\infty }(I)$
with uniform closure
![]() $\bar A$
, the maximal ideal spaces
$\bar A$
, the maximal ideal spaces
![]() $\mathfrak M(A)$
and
$\mathfrak M(A)$
and
![]() $\mathfrak M(\bar A)$
are homeomorphic (see, e.g., [Reference Royden19, Proposition 3]).
$\mathfrak M(\bar A)$
are homeomorphic (see, e.g., [Reference Royden19, Proposition 3]).
Example 1.5 (1) As a Banach algebra,
![]() $BV(I)=\ell ^1(I)\rtimes BV_+(I)$
—the semidirect product of the closed ideal
$BV(I)=\ell ^1(I)\rtimes BV_+(I)$
—the semidirect product of the closed ideal
![]() $\ell ^1(I)$
and the Banach subalgebra
$\ell ^1(I)$
and the Banach subalgebra
![]() $BV_+(I)$
of right-continuous
$BV_+(I)$
of right-continuous
![]() $BV$
functions (see, e.g., [Reference Brudnyi and Brudnyi6, Corollary 2.2]). Thus, the uniform closure
$BV$
functions (see, e.g., [Reference Brudnyi and Brudnyi6, Corollary 2.2]). Thus, the uniform closure
![]() $\overline {BV(I)}=c_0(I)\rtimes R_+(I)$
—the semidirect product of the closed ideal
$\overline {BV(I)}=c_0(I)\rtimes R_+(I)$
—the semidirect product of the closed ideal
![]() $c_0(I)$
of functions with at most countable supports converging to
$c_0(I)$
of functions with at most countable supports converging to
![]() $0$
and the Banach subalgebra
$0$
and the Banach subalgebra
![]() ${R_+(I)\subset \ell ^{\infty }(I)}$
of right-continuous functions having first kind discontinuities. Then each homomorphism in
${R_+(I)\subset \ell ^{\infty }(I)}$
of right-continuous functions having first kind discontinuities. Then each homomorphism in
![]() $\mathfrak M(\overline {BV(I)})$
is uniquely determined by its restrictions to
$\mathfrak M(\overline {BV(I)})$
is uniquely determined by its restrictions to
![]() $c_0(I)$
and
$c_0(I)$
and
![]() $R_+(I)$
. This leads to a continuous injection
$R_+(I)$
. This leads to a continuous injection
![]() $r:\mathfrak M(\overline {BV(I)})\to \mathfrak M(c(I))\times \mathfrak M(R_+(I))$
, where
$r:\mathfrak M(\overline {BV(I)})\to \mathfrak M(c(I))\times \mathfrak M(R_+(I))$
, where
![]() $c(I):={\mathbb C}\cdot 1_I\oplus c_0(I)$
. Next,
$c(I):={\mathbb C}\cdot 1_I\oplus c_0(I)$
. Next,
![]() $\mathfrak M(c(I))$
is homeomorphic to the one-pointed compactification of the discrete set I. In particular,
$\mathfrak M(c(I))$
is homeomorphic to the one-pointed compactification of the discrete set I. In particular,
![]() $\mathrm {dim}\,\mathfrak M(c(I))=0$
. In turn, there is a continuous surjection
$\mathrm {dim}\,\mathfrak M(c(I))=0$
. In turn, there is a continuous surjection
![]() $p: \mathfrak M(R_+(I))\to \mathfrak M(C(I))=I$
, the transpose of the embedding
$p: \mathfrak M(R_+(I))\to \mathfrak M(C(I))=I$
, the transpose of the embedding
![]() $C(I)\hookrightarrow R_+(I)$
, whose fibres consist of two points over interior points of I and of one point over the endpoints of I. (Specifically, if
$C(I)\hookrightarrow R_+(I)$
, whose fibres consist of two points over interior points of I and of one point over the endpoints of I. (Specifically, if
![]() $\varphi \in p^{-1}(x)$
, then
$\varphi \in p^{-1}(x)$
, then
![]() $\varphi (f)$
is equal either to
$\varphi (f)$
is equal either to
![]() $f(x^-)$
or to
$f(x^-)$
or to
![]() $f(x^+)$
.) Moreover,
$f(x^+)$
.) Moreover,
![]() $\mathrm {dim}\,\mathfrak M(R_+(I))=0$
(see, e.g., [Reference Brudnyi and Kinzebulatov7, Theorem 1.7]). These imply that r embeds
$\mathrm {dim}\,\mathfrak M(R_+(I))=0$
(see, e.g., [Reference Brudnyi and Kinzebulatov7, Theorem 1.7]). These imply that r embeds
![]() $\mathfrak M(\overline {BV(I)})$
into the zero-dimensional compact Hausdorff space
$\mathfrak M(\overline {BV(I)})$
into the zero-dimensional compact Hausdorff space
![]() $\mathfrak M(c(I))\times \mathfrak M(R_+(I))$
; hence,
$\mathfrak M(c(I))\times \mathfrak M(R_+(I))$
; hence,
![]() $\mathrm {dim}\,\mathfrak M(BV(I))=\mathrm { dim}\,\mathfrak M(\overline {BV(I)})=0$
and
$\mathrm {dim}\,\mathfrak M(BV(I))=\mathrm { dim}\,\mathfrak M(\overline {BV(I)})=0$
and
![]() $H^i(\mathfrak M(BV(I)),\mathbb {Z} )=0$
for all
$H^i(\mathfrak M(BV(I)),\mathbb {Z} )=0$
for all
![]() $i\in \mathbb {N}$
.
$i\in \mathbb {N}$
.
(2) If A is one of the algebras (b),(c), or (d) of Example 1.3, then
![]() $\mathfrak M(\bar A)$
is homeomorphic to I and, hence,
$\mathfrak M(\bar A)$
is homeomorphic to I and, hence,
![]() $\mathrm {dim}\, \mathfrak M(\bar A)=1$
and
$\mathrm {dim}\, \mathfrak M(\bar A)=1$
and
![]() $H^i(\mathfrak M(\bar A),\mathbb {Z} )=0$
for all
$H^i(\mathfrak M(\bar A),\mathbb {Z} )=0$
for all
![]() $i\in \mathbb {N}$
.
$i\in \mathbb {N}$
.
(3) If A is a weakly inverse-closed algebra generated by
![]() $f_1,\dots , f_n\in BV(I)$
, then
$f_1,\dots , f_n\in BV(I)$
, then
![]() $\mathfrak M(A)$
is homeomorphic to the polynomially convex hull of the range of
$\mathfrak M(A)$
is homeomorphic to the polynomially convex hull of the range of
![]() $(f_1,\dots , f_n): I\to {\mathbb C}^n$
described by the Alexander theorem [Reference Alexander1] presented in the next section (see, e.g., [Reference Royden19, Proposition 1] and [Reference Gamelin14, Chapter III, Theorem 1.4]).
$(f_1,\dots , f_n): I\to {\mathbb C}^n$
described by the Alexander theorem [Reference Alexander1] presented in the next section (see, e.g., [Reference Royden19, Proposition 1] and [Reference Gamelin14, Chapter III, Theorem 1.4]).
1.3
In the sequel,
![]() $\mathscr H^1$
denotes the Hausdorff one-dimensional measure. Furthermore,
$\mathscr H^1$
denotes the Hausdorff one-dimensional measure. Furthermore,
stands for the polynomially convex hull of a bounded subset
![]() $K\subset {\mathbb C}^n$
. If
$K\subset {\mathbb C}^n$
. If
![]() $X\Subset {\mathbb C}^n$
, then
$X\Subset {\mathbb C}^n$
, then
![]() $P(X)\subset C(X)$
denotes the uniform closure of the restriction of polynomials
$P(X)\subset C(X)$
denotes the uniform closure of the restriction of polynomials
![]() ${\mathbb C} [z_1,\dots , z_n]|_X$
. A compact connected subset of
${\mathbb C} [z_1,\dots , z_n]|_X$
. A compact connected subset of
![]() ${\mathbb C}^n$
is called a continuum.
${\mathbb C}^n$
is called a continuum.
The following result is due to Alexander [Reference Alexander1, Theorem 1].
Theorem A Suppose that
![]() $\Gamma \subset {\mathbb C}^n$
is a compact subset of a continuum of finite
$\Gamma \subset {\mathbb C}^n$
is a compact subset of a continuum of finite
![]() $\mathscr H^1$
-measure. Then
$\mathscr H^1$
-measure. Then
![]() $\widehat {\Gamma }\setminus \Gamma $
is a (possibly empty) pure one-dimensional complex analytic subset of
$\widehat {\Gamma }\setminus \Gamma $
is a (possibly empty) pure one-dimensional complex analytic subset of
![]() ${\mathbb C}^n\setminus \Gamma $
. If
${\mathbb C}^n\setminus \Gamma $
. If
![]() $H^1(\Gamma ,\mathbb {Z} )=0$
, then
$H^1(\Gamma ,\mathbb {Z} )=0$
, then
![]() $\widehat \Gamma =\Gamma $
and
$\widehat \Gamma =\Gamma $
and
![]() $P(\Gamma )=C(\Gamma )$
.
$P(\Gamma )=C(\Gamma )$
.
For historical remarks and further developments related to this theorem, see [Reference Stout21].
Using Theorem A, we prove the following.
Theorem 1.6 Suppose that
![]() $\Gamma \subset {\mathbb C}^n$
is a compact subset of a continuum of finite
$\Gamma \subset {\mathbb C}^n$
is a compact subset of a continuum of finite
![]() $\mathscr H^1$
-measure. Then (a)
$\mathscr H^1$
-measure. Then (a)
![]() $\mathrm {dim}\,\widehat \Gamma \le 2$
and (b)
$\mathrm {dim}\,\widehat \Gamma \le 2$
and (b)
![]() $H^2(\widehat \Gamma ,\mathbb {Z} )=0$
.
$H^2(\widehat \Gamma ,\mathbb {Z} )=0$
.
Theorem 1.6 describes the algebraic–topological structure of the polynomial convex hull in the Alexander theorem and fills a gap in this area of study. Theorem 1.4 is derived from Theorem 1.6.
The proof of Theorem 1.6 goes along the following lines. Part (a) of the theorem follows from Theorem A by virtue of some standard results of dimension theory. Then, using that a continuum with finite
![]() $\mathscr H^1$
-measure in
$\mathscr H^1$
-measure in
![]() ${\mathbb C}^n$
is contained in a rectifiable curve (see, e.g., [Reference Falconer13, Chapter 3]), part (b) of the theorem reduces to a similar result for the cohomology of the maximal ideal space
${\mathbb C}^n$
is contained in a rectifiable curve (see, e.g., [Reference Falconer13, Chapter 3]), part (b) of the theorem reduces to a similar result for the cohomology of the maximal ideal space
![]() $\mathfrak M(A)$
of a closed finitely generated subalgebra
$\mathfrak M(A)$
of a closed finitely generated subalgebra
![]() $A\subset \mathrm {Lip}(I)$
. Each such A is weakly inverse-closed. Therefore,
$A\subset \mathrm {Lip}(I)$
. Each such A is weakly inverse-closed. Therefore,
![]() $\mathfrak M(A)$
is homeomorphic to the polynomially convex hull of a rectifiable curve in some
$\mathfrak M(A)$
is homeomorphic to the polynomially convex hull of a rectifiable curve in some
![]() ${\mathbb C}^n$
which is the image of I under the map
${\mathbb C}^n$
which is the image of I under the map
![]() $I\to {\mathbb C}^n$
whose coordinates are generators of A. Then, part (a) of the theorem implies that
$I\to {\mathbb C}^n$
whose coordinates are generators of A. Then, part (a) of the theorem implies that
![]() $\mathrm {dim}\,\mathfrak M(A)\le 2$
. In turn, due to the Novodvorskii–Taylor theory [Reference Taylor23], to prove that
$\mathrm {dim}\,\mathfrak M(A)\le 2$
. In turn, due to the Novodvorskii–Taylor theory [Reference Taylor23], to prove that
![]() $H^2(\mathfrak M(A),\mathbb {Z} )=0$
under the condition
$H^2(\mathfrak M(A),\mathbb {Z} )=0$
under the condition
![]() $\mathrm {dim}\,\mathfrak M(A)\le 2$
, one must show that
$\mathrm {dim}\,\mathfrak M(A)\le 2$
, one must show that
![]() $2\times 2$
matrix idempotents of rank
$2\times 2$
matrix idempotents of rank
![]() $1$
with entries in A are similar over A to constant idempotents. The space of such idempotents over
$1$
with entries in A are similar over A to constant idempotents. The space of such idempotents over
![]() ${\mathbb C}$
is a two-dimensional complex algebraic subvariety of
${\mathbb C}$
is a two-dimensional complex algebraic subvariety of
![]() ${\mathbb C}^4$
of the form
${\mathbb C}^4$
of the form
![]() $X_1\sqcup X_2\sqcup X_3$
such that
$X_1\sqcup X_2\sqcup X_3$
such that
![]() $X_1\cong X_2\cong {\mathbb C}$
and the projection
$X_1\cong X_2\cong {\mathbb C}$
and the projection
![]() ${\mathbb C}^4\to {\mathbb C}^2$
onto the first two coordinates is constant along
${\mathbb C}^4\to {\mathbb C}^2$
onto the first two coordinates is constant along
![]() $X_1$
and
$X_1$
and
![]() $X_2$
and maps
$X_2$
and maps
![]() $X_3$
biholomorphically onto
$X_3$
biholomorphically onto
![]() ${\mathbb C}\times {\mathbb C}^*$
, where
${\mathbb C}\times {\mathbb C}^*$
, where
![]() ${\mathbb C}^*:={\mathbb C}\setminus \{0\}$
. Using this, Theorem A, and part (a) of the theorem, we deduce that
${\mathbb C}^*:={\mathbb C}\setminus \{0\}$
. Using this, Theorem A, and part (a) of the theorem, we deduce that
![]() $H^2(\mathfrak M(A),\mathbb {Z} )=0$
from the known result on the vanishing of two cohomology of a polynomially convex subset of
$H^2(\mathfrak M(A),\mathbb {Z} )=0$
from the known result on the vanishing of two cohomology of a polynomially convex subset of
![]() ${\mathbb C}^2$
(see, e.g., [Reference Stout21, Chapter 2.3]).
${\mathbb C}^2$
(see, e.g., [Reference Stout21, Chapter 2.3]).
2 Proof of Theorem 1.6
(a) Let
![]() $\mathrm {dim}_{\mathscr H}$
denote the Hausdorff dimension. By the Szpilrajn theorem (see, e.g., [Reference Heinonen15, pp. 62–63]) and because
$\mathrm {dim}_{\mathscr H}$
denote the Hausdorff dimension. By the Szpilrajn theorem (see, e.g., [Reference Heinonen15, pp. 62–63]) and because
![]() $\mathscr H^1(\Gamma )<\infty $
,
$\mathscr H^1(\Gamma )<\infty $
,
In turn, as
![]() $\widehat \Gamma \setminus \Gamma \ne \emptyset $
is a one-dimensional complex analytic space, its compact subsets have covering dimension
$\widehat \Gamma \setminus \Gamma \ne \emptyset $
is a one-dimensional complex analytic space, its compact subsets have covering dimension
![]() $\le 2$
. These imply that
$\le 2$
. These imply that
![]() $\mathrm {dim}\,\widehat \Gamma \le 2$
(see, e.g., [Reference Nagami18, Chapter 2, Theorems 9–11]).
$\mathrm {dim}\,\widehat \Gamma \le 2$
(see, e.g., [Reference Nagami18, Chapter 2, Theorems 9–11]).
(b) In the proof, we use the following results.
Lemma 2.1 Let A be a weakly inverse-closed complex Banach function algebra on a set X. Then every closed unital subalgebra
![]() $B\subset A$
is weakly inverse-closed.
$B\subset A$
is weakly inverse-closed.
Proof Suppose that
![]() $f\in B$
is such that
$f\in B$
is such that
![]() $\sup _X |f|<1$
. Since the algebra
$\sup _X |f|<1$
. Since the algebra
![]() $ A$
is weakly inverse-closed,
$ A$
is weakly inverse-closed,
![]() $\frac {1}{1-f}\in A$
. Also, the function
$\frac {1}{1-f}\in A$
. Also, the function
![]() $\frac {1}{1-f}$
is the sum of the uniformly convergent on X series
$\frac {1}{1-f}$
is the sum of the uniformly convergent on X series
![]() $\sum _{k=0}^{\infty } f^k$
. By the formula for the spectral radius of f (see, e.g., [Reference Gamelin14, Chapter I, Theorem 5.2]),
$\sum _{k=0}^{\infty } f^k$
. By the formula for the spectral radius of f (see, e.g., [Reference Gamelin14, Chapter I, Theorem 5.2]),
here,
![]() $\hat {f}$
is the Gelfand transform of f and
$\hat {f}$
is the Gelfand transform of f and
![]() $\lVert\cdot\rVert$
is the norm on
$\lVert\cdot\rVert$
is the norm on
![]() $ A$
.
$ A$
.
On the other hand, since
![]() $ A$
is weakly inverse-closed, [Reference Royden19, Proposition 1] implies that
$ A$
is weakly inverse-closed, [Reference Royden19, Proposition 1] implies that
Combining (2.2) and (2.3), we get for some
![]() $c\in (\sup _X |f|, 1)$
and all sufficiently large
$c\in (\sup _X |f|, 1)$
and all sufficiently large
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
This shows that the partial sums of the series
![]() $\sum _{k=0}^{\infty } f^k$
form a Cauchy sequence in
$\sum _{k=0}^{\infty } f^k$
form a Cauchy sequence in
![]() $ A$
. Since these partial sums belong to the closed subalgebra
$ A$
. Since these partial sums belong to the closed subalgebra
![]() $B\subset A$
, the series converges to an element of B. This implies that
$B\subset A$
, the series converges to an element of B. This implies that
![]() $\frac {1}{1-f}\in B$
, as required.
$\frac {1}{1-f}\in B$
, as required.
Proposition 2.2 Suppose that
![]() $\mathcal A$
is a complex Banach function algebra defined on its maximal ideal space
$\mathcal A$
is a complex Banach function algebra defined on its maximal ideal space
![]() $\mathfrak M(\mathcal A)$
. If
$\mathfrak M(\mathcal A)$
. If
![]() $\mathrm {dim}\,\mathfrak M(\mathcal A)\le 2$
, then there are bijections:
$\mathrm {dim}\,\mathfrak M(\mathcal A)\le 2$
, then there are bijections:
-
(a)
 $c_1:\mathrm {Vect}_1(\mathfrak M(\mathcal A))\to H^2(\mathfrak M(\mathcal A),\mathbb {Z} )$
, where
$c_1:\mathrm {Vect}_1(\mathfrak M(\mathcal A))\to H^2(\mathfrak M(\mathcal A),\mathbb {Z} )$
, where
 $\mathrm {Vect}_1(\mathfrak M(\mathcal A))$
is the set of isomorphism classes of complex rank-1 vector bundles over
$\mathrm {Vect}_1(\mathfrak M(\mathcal A))$
is the set of isomorphism classes of complex rank-1 vector bundles over
 $\mathfrak M(\mathcal A)$
.
$\mathfrak M(\mathcal A)$
. -
(b)
 $h: [\mathfrak M(\mathcal A),\mathbb S^2]\to H^2(\mathfrak M(\mathcal A),\mathbb {Z} )$
, where
$h: [\mathfrak M(\mathcal A),\mathbb S^2]\to H^2(\mathfrak M(\mathcal A),\mathbb {Z} )$
, where
 $[\mathfrak M(\mathcal A),\mathbb S^2]$
is the set of homotopy classes of continuous maps from
$[\mathfrak M(\mathcal A),\mathbb S^2]$
is the set of homotopy classes of continuous maps from
 $\mathfrak M(\mathcal A)$
to the two-dimensional unit sphere
$\mathfrak M(\mathcal A)$
to the two-dimensional unit sphere
 $\mathbb S^2$
.
$\mathbb S^2$
. -
(c)
 $i:[\mathrm {ID}_1(\mathcal A_2)]\to [\mathfrak M(\mathcal A),\mathbb S^2]$
, where
$i:[\mathrm {ID}_1(\mathcal A_2)]\to [\mathfrak M(\mathcal A),\mathbb S^2]$
, where
 $[\mathrm {ID}_1(\mathcal A_2)]$
is the set of connectivity components of the class of idempotent
$[\mathrm {ID}_1(\mathcal A_2)]$
is the set of connectivity components of the class of idempotent
 $2\times 2$
matrices with entries in
$2\times 2$
matrices with entries in
 $\mathcal A$
of constant rank
$\mathcal A$
of constant rank
 $1$
.
$1$
.
Proof In (a) and (c), the condition
![]() $\mathrm {dim}\,\mathfrak M(\mathcal A)\le 2$
is not required. In fact, the bijection
$\mathrm {dim}\,\mathfrak M(\mathcal A)\le 2$
is not required. In fact, the bijection
![]() $c_1$
is determined by assigning to a bundle its first Chern class, whereas the existence of the bijection i follows from the Novodvorskii–Taylor theory (see [Reference Taylor23, Section 5.3, p. 186]). Finally, the existence of the bijection h under the condition
$c_1$
is determined by assigning to a bundle its first Chern class, whereas the existence of the bijection i follows from the Novodvorskii–Taylor theory (see [Reference Taylor23, Section 5.3, p. 186]). Finally, the existence of the bijection h under the condition
![]() $\mathrm {dim}\,\mathfrak M(\mathcal A)\le 2$
follows from the Hopf theorem (see, e.g., [Reference Hu16]).
$\mathrm {dim}\,\mathfrak M(\mathcal A)\le 2$
follows from the Hopf theorem (see, e.g., [Reference Hu16]).
Let us proceed to the proof of part (b) of the theorem.
Let
![]() $E\subset {\mathbb C}^n$
be a continuum with
$E\subset {\mathbb C}^n$
be a continuum with
![]() $\mathscr H^1(E)<\infty $
containing
$\mathscr H^1(E)<\infty $
containing
![]() $\Gamma $
. Then, according to [Reference Falconer13, Chapter 3, Exercise 3.5], there are functions
$\Gamma $
. Then, according to [Reference Falconer13, Chapter 3, Exercise 3.5], there are functions
![]() $f_1,\dots , f_{n}\in \mathrm {Lip}(I)$
such that
$f_1,\dots , f_{n}\in \mathrm {Lip}(I)$
such that
By
![]() $A\subset \mathrm {Lip}(I)$
, we denote the closed unital subalgebra generated by
$A\subset \mathrm {Lip}(I)$
, we denote the closed unital subalgebra generated by
![]() $f_1,\dots , f_{n}$
. Since it is clear that
$f_1,\dots , f_{n}$
. Since it is clear that
![]() $\mathrm {Lip}(I)$
is weakly inverse-closed, by Lemma 2.1, A is also weakly inverse-closed. Then the maximal ideal space of A is naturally identified with
$\mathrm {Lip}(I)$
is weakly inverse-closed, by Lemma 2.1, A is also weakly inverse-closed. Then the maximal ideal space of A is naturally identified with
![]() $\widehat K$
(see, e.g., [Reference Royden19, Proposition 1] and [Reference Gamelin14, Chapter III, Theorem 1.4]). Moreover, according to part (a) of the theorem,
$\widehat K$
(see, e.g., [Reference Royden19, Proposition 1] and [Reference Gamelin14, Chapter III, Theorem 1.4]). Moreover, according to part (a) of the theorem,
![]() $\mathrm {dim}\,\widehat K\le 2$
.
$\mathrm {dim}\,\widehat K\le 2$
.
We set
![]() $F:=(f_1,\dots , f_n): I\to {\mathbb C}^n$
. The algebra A is isomorphic to its Gelfand transform
$F:=(f_1,\dots , f_n): I\to {\mathbb C}^n$
. The algebra A is isomorphic to its Gelfand transform
![]() $\hat {A}$
—a complex Banach function algebra on
$\hat {A}$
—a complex Banach function algebra on
![]() $\widehat K=\mathfrak M(A)$
with a norm induced from A such that the pullback of
$\widehat K=\mathfrak M(A)$
with a norm induced from A such that the pullback of
![]() $\hat A$
by F coincides with A (hence,
$\hat A$
by F coincides with A (hence,
![]() ${\mathbb C} [z_1,\dots , z_n]|_{\widehat K}$
is a dense subalgebra of
${\mathbb C} [z_1,\dots , z_n]|_{\widehat K}$
is a dense subalgebra of
![]() $\hat A$
). Since
$\hat A$
). Since
![]() $\mathfrak M(\hat A)=\widehat K$
as well, in the notation of Proposition 2.2, each
$\mathfrak M(\hat A)=\widehat K$
as well, in the notation of Proposition 2.2, each
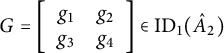 $$ \begin{align} G=\left[ \begin{array}{cc} g_1&g_2\\ g_3&g_4 \end{array} \right]\in \mathrm{ID}_1(\hat A_2) \end{align} $$
$$ \begin{align} G=\left[ \begin{array}{cc} g_1&g_2\\ g_3&g_4 \end{array} \right]\in \mathrm{ID}_1(\hat A_2) \end{align} $$
can be viewed as a map from
![]() $\widehat K$
to
$\widehat K$
to
![]() $M_2({\mathbb C})$
with coordinates in the algebra
$M_2({\mathbb C})$
with coordinates in the algebra
![]() $\hat A$
whose image
$\hat A$
whose image
![]() $\mathrm {ID}_1({\mathbb C}_2)$
consists of idempotent matrices of rank
$\mathrm {ID}_1({\mathbb C}_2)$
consists of idempotent matrices of rank
![]() $1$
. Thus,
$1$
. Thus,
 $$\begin{align*}Z=\left[ \begin{array}{cc} z_1&z_2\\ z_3&z_4 \end{array} \right] \in \mathrm{ID}_1({\mathbb C}_2) \end{align*}$$
$$\begin{align*}Z=\left[ \begin{array}{cc} z_1&z_2\\ z_3&z_4 \end{array} \right] \in \mathrm{ID}_1({\mathbb C}_2) \end{align*}$$
if and only if
![]() $\mathrm {rank}\, Z=1$
and
$\mathrm {rank}\, Z=1$
and
 $$\begin{align*}Z^2-Z=\left[ \begin{array}{ccc} z_1&z_2\\ z_3&z_4 \end{array} \right]\cdot \left[ \begin{array}{ccc} z_1-1&z_2\\ z_3&z_4-1 \end{array} \right]= \left[ \begin{array}{ccc} 0&0\\ 0&0 \end{array} \right], \end{align*}$$
$$\begin{align*}Z^2-Z=\left[ \begin{array}{ccc} z_1&z_2\\ z_3&z_4 \end{array} \right]\cdot \left[ \begin{array}{ccc} z_1-1&z_2\\ z_3&z_4-1 \end{array} \right]= \left[ \begin{array}{ccc} 0&0\\ 0&0 \end{array} \right], \end{align*}$$
which implies that
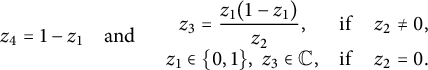 $$ \begin{align} z_4=1-z_1\quad \mathrm{and}\quad \begin{array}{ccc} \displaystyle z_3=\frac{z_1(1-z_1)}{z_2},&\mathrm{if}&z_2\ne 0,\\[4pt] z_1\in\{0,1\},\ z_3\in{\mathbb C},&\mathrm{if}&z_2=0. \end{array} \end{align} $$
$$ \begin{align} z_4=1-z_1\quad \mathrm{and}\quad \begin{array}{ccc} \displaystyle z_3=\frac{z_1(1-z_1)}{z_2},&\mathrm{if}&z_2\ne 0,\\[4pt] z_1\in\{0,1\},\ z_3\in{\mathbb C},&\mathrm{if}&z_2=0. \end{array} \end{align} $$
Let
![]() $S:=G(K)=(G\circ F)(I)\subset M_2({\mathbb C})\cong {\mathbb C}^4$
. Since the entries of the map
$S:=G(K)=(G\circ F)(I)\subset M_2({\mathbb C})\cong {\mathbb C}^4$
. Since the entries of the map
![]() $G\circ F$
lie in
$G\circ F$
lie in
![]() $\mathrm {Lip}(I)$
, S is a continuum with
$\mathrm {Lip}(I)$
, S is a continuum with
![]() $\mathscr H^1(S)<\infty $
. Moreover,
$\mathscr H^1(S)<\infty $
. Moreover,
![]() $\hat A$
is contained in the uniform closure of
$\hat A$
is contained in the uniform closure of
![]() ${\mathbb C} [z_1,\dots , z_n]|_{\widehat K}$
, which implies that
${\mathbb C} [z_1,\dots , z_n]|_{\widehat K}$
, which implies that
![]() $G(\widehat K)\subset \widehat S\subset \mathrm {ID}_1({\mathbb C}_2)$
. In addition,
$G(\widehat K)\subset \widehat S\subset \mathrm {ID}_1({\mathbb C}_2)$
. In addition,
![]() $\mathrm {dim}\,\widehat S\le 2$
by part (a) of the theorem. By the definition, the identity map
$\mathrm {dim}\,\widehat S\le 2$
by part (a) of the theorem. By the definition, the identity map
![]() ${\mathbb C}^4 \supset \mathrm {ID}_1({\mathbb C}_2)\to \mathrm {ID}_1({\mathbb C}_2)\subset M_2({\mathbb C})$
determines the holomorphic idempotent Z on
${\mathbb C}^4 \supset \mathrm {ID}_1({\mathbb C}_2)\to \mathrm {ID}_1({\mathbb C}_2)\subset M_2({\mathbb C})$
determines the holomorphic idempotent Z on
![]() $\mathrm {ID}_1({\mathbb C}_2)$
whose pullback by G coincides with
$\mathrm {ID}_1({\mathbb C}_2)$
whose pullback by G coincides with
![]() $G\in \mathrm {ID}_1(\hat A_2)$
. According to Proposition 2.2,
$G\in \mathrm {ID}_1(\hat A_2)$
. According to Proposition 2.2,
![]() $Z|_{\widehat S}$
determines a complex rank-1 vector bundle over
$Z|_{\widehat S}$
determines a complex rank-1 vector bundle over
![]() $\widehat S$
whose triviality implies that
$\widehat S$
whose triviality implies that
![]() $Z|_{\widehat S}$
and, hence, G belong to the connectivity components (in
$Z|_{\widehat S}$
and, hence, G belong to the connectivity components (in
![]() $\mathrm {ID}_1(C(\widehat S)_2)$
and
$\mathrm {ID}_1(C(\widehat S)_2)$
and
![]() $\mathrm {ID}_1(\hat A_2)$
, respectively) of the constant idempotent
$\mathrm {ID}_1(\hat A_2)$
, respectively) of the constant idempotent
![]() $I_1\oplus 0_1$
. If the latter is true for all
$I_1\oplus 0_1$
. If the latter is true for all
![]() $G\in \mathrm {ID}_1(\hat A_2)$
, then Proposition 2.2 implies that
$G\in \mathrm {ID}_1(\hat A_2)$
, then Proposition 2.2 implies that
![]() $H^2(\widehat K,\mathbb {Z} )=0$
. However,
$H^2(\widehat K,\mathbb {Z} )=0$
. However,
![]() $\widehat {\Gamma }\subset \widehat K$
and
$\widehat {\Gamma }\subset \widehat K$
and
![]() $\mathrm {dim}\,\widehat K\le 2$
and so the previous condition implies that
$\mathrm {dim}\,\widehat K\le 2$
and so the previous condition implies that
![]() $H^2(\widehat \Gamma ,\mathbb {Z} )=0$
by the Hopf theorem, as required. Thus, to complete the proof of the theorem, it suffices to prove the following lemma.
$H^2(\widehat \Gamma ,\mathbb {Z} )=0$
by the Hopf theorem, as required. Thus, to complete the proof of the theorem, it suffices to prove the following lemma.
Lemma 2.3 Each complex rank-1 vector bundle over
![]() $\widehat S$
is trivial.
$\widehat S$
is trivial.
Proof Let V be a complex rank-1 vector bundle over
![]() $\widehat S$
. Consider the projection onto the first two coordinates
$\widehat S$
. Consider the projection onto the first two coordinates
![]() $\pi : {\mathbb C}^4\to {\mathbb C}^2$
and
$\pi : {\mathbb C}^4\to {\mathbb C}^2$
and
![]() $\pi (z_1,z_2,z_3, z_4):=(z_1,z_2)$
. For
$\pi (z_1,z_2,z_3, z_4):=(z_1,z_2)$
. For
![]() ${w_i=(i,0)}$
,
${w_i=(i,0)}$
,
![]() $i=0,1$
, the sets
$i=0,1$
, the sets
![]() $ \pi ^{-1}(w_i)\cap \mathrm {ID}_1({\mathbb C}_2)$
are biholomorphic to
$ \pi ^{-1}(w_i)\cap \mathrm {ID}_1({\mathbb C}_2)$
are biholomorphic to
![]() ${\mathbb C}$
(see (2.6)). Thus,
${\mathbb C}$
(see (2.6)). Thus,
![]() $Z_i:=\pi ^{-1}(w_i)\cap \widehat S$
are homeomorphic to compact subsets of
$Z_i:=\pi ^{-1}(w_i)\cap \widehat S$
are homeomorphic to compact subsets of
![]() ${\mathbb C}$
; hence,
${\mathbb C}$
; hence,
![]() $H^2(Z_i,\mathbb {Z} )=0$
,
$H^2(Z_i,\mathbb {Z} )=0$
,
![]() $i=0,1$
. This implies that
$i=0,1$
. This implies that
![]() $V|_{Z_i}$
are trivial bundles. In particular, there are disjoint open neighborhoods
$V|_{Z_i}$
are trivial bundles. In particular, there are disjoint open neighborhoods
![]() $U_i\subset \widehat S$
of
$U_i\subset \widehat S$
of
![]() $Z_i$
and nonvanishing continuous sections
$Z_i$
and nonvanishing continuous sections
![]() $s_i:U_i\to V$
,
$s_i:U_i\to V$
,
![]() ${i=0,1}$
. Since
${i=0,1}$
. Since
where
![]() $\mathcal N(w_i)$
is the set of all open neighborhoods of
$\mathcal N(w_i)$
is the set of all open neighborhoods of
![]() $w_i$
, without loss of generality, we may assume that
$w_i$
, without loss of generality, we may assume that
![]() $U_i=\pi ^{-1}(O_i)\cap \widehat S$
for some
$U_i=\pi ^{-1}(O_i)\cap \widehat S$
for some
![]() $O_i\in \mathcal N(w_i)$
,
$O_i\in \mathcal N(w_i)$
,
![]() $i=0,1$
. Let
$i=0,1$
. Let
![]() $U_2,\dots , U_k$
be relatively compact open subsets of
$U_2,\dots , U_k$
be relatively compact open subsets of
![]() $\widehat S\setminus \pi ^{-1}(w_i)$
such that
$\widehat S\setminus \pi ^{-1}(w_i)$
such that
![]() $(U_i)_{i=0}^k$
is an open cover of
$(U_i)_{i=0}^k$
is an open cover of
![]() $\widehat S$
and each
$\widehat S$
and each
![]() $V|_{U_i}$
is trivial. Due to (2.6),
$V|_{U_i}$
is trivial. Due to (2.6),
![]() $\pi $
maps
$\pi $
maps
![]() $\widehat S\setminus (\pi ^{-1}(w_0)\cup \pi ^{-1}(w_1))$
homeomorphically onto
$\widehat S\setminus (\pi ^{-1}(w_0)\cup \pi ^{-1}(w_1))$
homeomorphically onto
![]() $\pi (\widehat S)\setminus \{w_0,w_1\}$
. Thus, there exist (relatively compact) open subsets
$\pi (\widehat S)\setminus \{w_0,w_1\}$
. Thus, there exist (relatively compact) open subsets
![]() $O_i\subset \pi (\widehat S)\setminus \{w_0,w_1\}$
,
$O_i\subset \pi (\widehat S)\setminus \{w_0,w_1\}$
,
![]() $2\le i\le k$
, such that
$2\le i\le k$
, such that
![]() $\pi ^{-1}(O_i)\cap \widehat S=U_i$
. Let
$\pi ^{-1}(O_i)\cap \widehat S=U_i$
. Let
![]() $s_i: U_i\to V$
be nonvanishing continuous sections of
$s_i: U_i\to V$
be nonvanishing continuous sections of
![]() $V|_{U_i}$
,
$V|_{U_i}$
,
![]() $i=2,\dots , k$
. Then V is determined by a continuous cocycle
$i=2,\dots , k$
. Then V is determined by a continuous cocycle
![]() $\{c_{ij}\}_{0\le i,j\le k}$
,
$\{c_{ij}\}_{0\le i,j\le k}$
,
Furthermore, since each nonvoid
![]() $U_i\cap U_j$
is a subset of
$U_i\cap U_j$
is a subset of
![]() $\widehat S\setminus (\pi ^{-1}(w_0)\cup \pi ^{-1}(w_1))$
, due to (2.6), there exist
$\widehat S\setminus (\pi ^{-1}(w_0)\cup \pi ^{-1}(w_1))$
, due to (2.6), there exist
![]() $d_{ij}\in C(O_i\cap O_j,{\mathbb C}^*)$
such that
$d_{ij}\in C(O_i\cap O_j,{\mathbb C}^*)$
such that
![]() $\pi ^{*}d_{ij}=c_{ij}$
. The family
$\pi ^{*}d_{ij}=c_{ij}$
. The family
![]() $\{d_{ij}\}_{0\le i,j\le k}$
is a
$\{d_{ij}\}_{0\le i,j\le k}$
is a
![]() $1$
cocycle on the cover
$1$
cocycle on the cover
![]() $(O_i)_{0\le i\le k}$
of
$(O_i)_{0\le i\le k}$
of
![]() $\pi (\widehat S)$
, which determines a bundle
$\pi (\widehat S)$
, which determines a bundle
![]() $V'$
on
$V'$
on
![]() $\widehat S$
such that
$\widehat S$
such that
![]() $\pi ^*V'|_{\widehat S}=V$
. Thus, to complete the proof, it suffices to show that
$\pi ^*V'|_{\widehat S}=V$
. Thus, to complete the proof, it suffices to show that
![]() $V'$
is a trivial bundle.
$V'$
is a trivial bundle.
Indeed, by definition,
![]() $\pi (\widehat S)\subset \widehat {\pi (S)}\subset {\mathbb C}^2$
. Since S is a continuum with
$\pi (\widehat S)\subset \widehat {\pi (S)}\subset {\mathbb C}^2$
. Since S is a continuum with
![]() ${\mathscr H^1(S)<\infty }$
, the set
${\mathscr H^1(S)<\infty }$
, the set
![]() $\pi (S)=:(\pi \circ G\circ F)(I)$
is also a continuum with
$\pi (S)=:(\pi \circ G\circ F)(I)$
is also a continuum with
![]() $\mathscr H^1(\pi (S))<\infty $
and so part (a) of the theorem implies that
$\mathscr H^1(\pi (S))<\infty $
and so part (a) of the theorem implies that
![]() $\mathrm {dim}\, \widehat {\pi (S)}\le 2$
. In addition,
$\mathrm {dim}\, \widehat {\pi (S)}\le 2$
. In addition,
![]() $\widehat {\pi (S)}$
is a polynomially convex subset of
$\widehat {\pi (S)}$
is a polynomially convex subset of
![]() ${\mathbb C}^2$
; hence,
${\mathbb C}^2$
; hence,
![]() $H^2(\widehat {\pi (S)},\mathbb {Z} )=0$
(see, e.g., [Reference Stout21, Corollary 2.3.6]). These imply that
$H^2(\widehat {\pi (S)},\mathbb {Z} )=0$
(see, e.g., [Reference Stout21, Corollary 2.3.6]). These imply that
![]() $H^2(\pi (\widehat S),\mathbb {Z} )=0$
by the Hopf theorem. In particular, each complex rank-1 vector bundle over
$H^2(\pi (\widehat S),\mathbb {Z} )=0$
by the Hopf theorem. In particular, each complex rank-1 vector bundle over
![]() $\pi (\widehat S)$
is trivial; hence, the bundle
$\pi (\widehat S)$
is trivial; hence, the bundle
![]() $V'$
is trivial as well, as required.
$V'$
is trivial as well, as required.
The proof of Theorem 1.6 is complete.
3 Proofs of Theorems 1.1, 1.2, and 1.4
Proof of Theorem 1.4
Let D be the set of all finite subsets of
![]() $A\cap BV(I)$
directed by inclusion
$A\cap BV(I)$
directed by inclusion
![]() $\subset $
. If
$\subset $
. If
![]() $\alpha =\{f_{1,\alpha },\dots , f_{k_{\alpha },\alpha }\}\in D$
, we let
$\alpha =\{f_{1,\alpha },\dots , f_{k_{\alpha },\alpha }\}\in D$
, we let
![]() $A_{\alpha }$
be the closed subalgebra of A generated by
$A_{\alpha }$
be the closed subalgebra of A generated by
![]() $\alpha $
. For
$\alpha $
. For
![]() $\alpha \subset \beta $
, we have
$\alpha \subset \beta $
, we have
![]() $A_{\alpha }\subset A_{\beta }$
and we denote by
$A_{\alpha }\subset A_{\beta }$
and we denote by
![]() $i_{\alpha }^{\beta }: A_{\alpha }\hookrightarrow A_{\beta }$
the corresponding inclusion map. Then
$i_{\alpha }^{\beta }: A_{\alpha }\hookrightarrow A_{\beta }$
the corresponding inclusion map. Then
![]() $\{A_{\alpha }, i_{\alpha }^{\beta }\}$
is the injective system whose limit
$\{A_{\alpha }, i_{\alpha }^{\beta }\}$
is the injective system whose limit
![]() $A_*:=\varinjlim A_{\alpha }$
is a subalgebra of A containing
$A_*:=\varinjlim A_{\alpha }$
is a subalgebra of A containing
![]() $A\cap BV(I)$
. In particular,
$A\cap BV(I)$
. In particular,
![]() $ A_*$
is dense in A by the hypothesis, and hence the same is true for the images of
$ A_*$
is dense in A by the hypothesis, and hence the same is true for the images of
![]() $A_*$
and A in
$A_*$
and A in
![]() $C(\mathfrak M(A))$
under the Gelfand transform. Since by the hypothesis A is weakly inverse-closed, the latter along with Propositions 3 and 9 of [Reference Royden19] imply that the maximal ideal space
$C(\mathfrak M(A))$
under the Gelfand transform. Since by the hypothesis A is weakly inverse-closed, the latter along with Propositions 3 and 9 of [Reference Royden19] imply that the maximal ideal space
![]() $\mathfrak M(A)=\varprojlim \mathfrak M(A_{\alpha })$
—the projective limit of the adjoint projective system
$\mathfrak M(A)=\varprojlim \mathfrak M(A_{\alpha })$
—the projective limit of the adjoint projective system
![]() $\{\mathfrak M(A_{\alpha }), (i_{\alpha }^{\beta })^*\}$
of the maximal ideal spaces. Since
$\{\mathfrak M(A_{\alpha }), (i_{\alpha }^{\beta })^*\}$
of the maximal ideal spaces. Since
![]() $A_{\alpha }$
is generated by
$A_{\alpha }$
is generated by
![]() $f_{1,\alpha },\dots , f_{k_{\alpha },\alpha }\in BV(I)$
, the range of the map
$f_{1,\alpha },\dots , f_{k_{\alpha },\alpha }\in BV(I)$
, the range of the map
![]() $F_{\alpha }=(f_{1,\alpha },\dots , f_{k_{\alpha },\alpha }): I\to {\mathbb C}^{k_{\alpha }}$
denoted by
$F_{\alpha }=(f_{1,\alpha },\dots , f_{k_{\alpha },\alpha }): I\to {\mathbb C}^{k_{\alpha }}$
denoted by
![]() $\Gamma _{\alpha }$
is contained in a continuum with finite
$\Gamma _{\alpha }$
is contained in a continuum with finite
![]() $\mathscr H^1$
measure (see, e.g., [Reference Falconer13, Chapter 3, Exercise 3.1]). Moreover, by Lemma 2.1,
$\mathscr H^1$
measure (see, e.g., [Reference Falconer13, Chapter 3, Exercise 3.1]). Moreover, by Lemma 2.1,
![]() $A_{\alpha }$
is weakly inverse-closed. Therefore,
$A_{\alpha }$
is weakly inverse-closed. Therefore,
![]() $\mathfrak M(A_{\alpha })$
is homeomorphic to
$\mathfrak M(A_{\alpha })$
is homeomorphic to
![]() $\widehat {\Gamma }_{\alpha }$
(see, e.g., [Reference Royden19, Proposition 1] and [Reference Gamelin14, Chapter III, Theorem 1.4]), and
$\widehat {\Gamma }_{\alpha }$
(see, e.g., [Reference Royden19, Proposition 1] and [Reference Gamelin14, Chapter III, Theorem 1.4]), and
![]() $\mathrm {dim}\,\widehat {\Gamma }_{\alpha }\le 2$
and
$\mathrm {dim}\,\widehat {\Gamma }_{\alpha }\le 2$
and
![]() $H^2(\widehat {\Gamma }_{\alpha },\mathbb {Z} )=0$
by Theorem 1.6. Then, since
$H^2(\widehat {\Gamma }_{\alpha },\mathbb {Z} )=0$
by Theorem 1.6. Then, since
![]() $\mathfrak M(A)=\varprojlim \mathfrak M(A_{\alpha })$
,
$\mathfrak M(A)=\varprojlim \mathfrak M(A_{\alpha })$
,
![]() $\mathrm {dim}\,\mathfrak M(A)\le 2$
(see, e.g., [Reference Engelking12, Theorem 3.3.6]), and
$\mathrm {dim}\,\mathfrak M(A)\le 2$
(see, e.g., [Reference Engelking12, Theorem 3.3.6]), and
![]() $H^2(\mathfrak M(A),\mathbb {Z} )=0$
(see, e.g., [Reference Eilenberg and Steenrod11, Theorem 3.1, p. 261]), as required.
$H^2(\mathfrak M(A),\mathbb {Z} )=0$
(see, e.g., [Reference Eilenberg and Steenrod11, Theorem 3.1, p. 261]), as required.
Proof of Theorem 1.1
Let M be a finitely generated projective A-module determined by an idempotent
![]() $I\in M_n(A)$
. The rank of M is a continuous
$I\in M_n(A)$
. The rank of M is a continuous
![]() $\mathbb {Z} _+$
-valued function on
$\mathbb {Z} _+$
-valued function on
![]() $\mathfrak M(A)$
equal to the rank of the Gelfand transform of I at points of
$\mathfrak M(A)$
equal to the rank of the Gelfand transform of I at points of
![]() $\mathfrak M(A)$
(see, e.g., [Reference Taylor23, Section 7.6]). Let
$\mathfrak M(A)$
(see, e.g., [Reference Taylor23, Section 7.6]). Let
![]() $0\le i_1<\cdots < i_k\le n$
be the range of this function, and let
$0\le i_1<\cdots < i_k\le n$
be the range of this function, and let
![]() $\mathfrak M_s\subset \mathfrak M(A)$
be the clopen subset where
$\mathfrak M_s\subset \mathfrak M(A)$
be the clopen subset where
![]() $\hat {I}$
has constant rank
$\hat {I}$
has constant rank
![]() $i_s$
. Then
$i_s$
. Then
![]() $\mathfrak M(A)=\sqcup _{s=1}^k\mathfrak M_s$
, and by the Shilov idempotent theory (see, e.g., [Reference Gamelin14, Chapter III, Corollary 6.5]), there exist idempotents
$\mathfrak M(A)=\sqcup _{s=1}^k\mathfrak M_s$
, and by the Shilov idempotent theory (see, e.g., [Reference Gamelin14, Chapter III, Corollary 6.5]), there exist idempotents
![]() $p_1,\dots , p_k\in A$
with
$p_1,\dots , p_k\in A$
with
![]() $\sum _{s=1}^k p_s= 1_A$
such that the maximal ideal space of
$\sum _{s=1}^k p_s= 1_A$
such that the maximal ideal space of
![]() $A_{p_s}$
is
$A_{p_s}$
is
![]() $\mathfrak M_s$
. We have
$\mathfrak M_s$
. We have
![]() $A=\oplus _{s=1}^k A_{p_s}$
, which leads to the decomposition
$A=\oplus _{s=1}^k A_{p_s}$
, which leads to the decomposition
![]() $I=\oplus _{s=1}^k\,p_s\cdot I$
, where
$I=\oplus _{s=1}^k\,p_s\cdot I$
, where
![]() $p_s\cdot I\in M_n(A_{p_s})$
is the idempotent determining the projective
$p_s\cdot I\in M_n(A_{p_s})$
is the idempotent determining the projective
![]() $A_{p_s}$
-module
$A_{p_s}$
-module
![]() $M_{p_s}$
.
$M_{p_s}$
.
Next, due to the Novodvorskii–Taylor theory (see [Reference Taylor23, Section 7.5, Theorem]), there exists a bijection between isomorphism classes of finitely generated projective
![]() $A_{p_s}$
-modules and complex vector bundles over
$A_{p_s}$
-modules and complex vector bundles over
![]() $\mathfrak M_s$
. In our case, the isomorphism class of
$\mathfrak M_s$
. In our case, the isomorphism class of
![]() $M_{p_s}$
corresponds to the isomorphism class of a bundle
$M_{p_s}$
corresponds to the isomorphism class of a bundle
![]() $E_s$
over
$E_s$
over
![]() $\mathfrak M_s$
of complex rank
$\mathfrak M_s$
of complex rank
![]() $i_s$
. Since
$i_s$
. Since
![]() $\mathrm {dim}\, \mathfrak M_s\le 2$
and
$\mathrm {dim}\, \mathfrak M_s\le 2$
and
![]() $H^2(\mathfrak M_s,\mathbb {Z} )=0$
by Theorem 1.4, the bundle
$H^2(\mathfrak M_s,\mathbb {Z} )=0$
by Theorem 1.4, the bundle
![]() $E_s$
is trivial (i.e., isomorphic to
$E_s$
is trivial (i.e., isomorphic to
![]() $\mathfrak M_s\times {\mathbb C}^{i_s}$
), which implies that
$\mathfrak M_s\times {\mathbb C}^{i_s}$
), which implies that
![]() $M_{p_s}$
is isomorphic to the free module
$M_{p_s}$
is isomorphic to the free module
![]() $(A_{p_s})^{i_s}$
, as required.
$(A_{p_s})^{i_s}$
, as required.
Proof of Theorem 1.2
Let
![]() $J\subset A\subset BV(I)$
be a closed ideal. Its hull
$J\subset A\subset BV(I)$
be a closed ideal. Its hull
![]() $\mathcal Z( J)\subset \mathfrak M(A)$
is given by
$\mathcal Z( J)\subset \mathfrak M(A)$
is given by
Consider the closed unital subalgebra
![]() $A_J:=\{c\cdot 1_A+f\,:\, c\in {\mathbb C},\ f\in J\}\subset A$
. By
$A_J:=\{c\cdot 1_A+f\,:\, c\in {\mathbb C},\ f\in J\}\subset A$
. By
![]() $Q_J: \mathfrak M(A)\rightarrow \mathfrak M(A_J)$
, we denote the continuous map transposed to the embedding
$Q_J: \mathfrak M(A)\rightarrow \mathfrak M(A_J)$
, we denote the continuous map transposed to the embedding
![]() $A_J\hookrightarrow A$
. Then
$A_J\hookrightarrow A$
. Then
![]() $Q_J$
is a surjection which is one-to-one on
$Q_J$
is a surjection which is one-to-one on
![]() $\mathfrak M(A)\setminus \mathcal Z(J)$
and sends
$\mathfrak M(A)\setminus \mathcal Z(J)$
and sends
![]() $\mathcal Z(J)$
to a point (see, e.g., [Reference Brudnyi3, Proposition 2.1] for the proof of a similar result). On the other hand,
$\mathcal Z(J)$
to a point (see, e.g., [Reference Brudnyi3, Proposition 2.1] for the proof of a similar result). On the other hand,
![]() $A_J\subset BV(I)$
is weakly inverse-closed by Lemma 2.1, and so by Theorem 1.4,
$A_J\subset BV(I)$
is weakly inverse-closed by Lemma 2.1, and so by Theorem 1.4,
![]() $\mathrm { dim}\,\mathfrak M(A_J)\le 2$
and
$\mathrm { dim}\,\mathfrak M(A_J)\le 2$
and
![]() $H^2(\mathfrak M(A_J),\mathbb {Z} )=0$
.
$H^2(\mathfrak M(A_J),\mathbb {Z} )=0$
.
According to [Reference Suárez22, Theorem 1.3], to prove that the stable rank of A is
![]() $1$
, it suffices to show that the relative Čech cohomology groups
$1$
, it suffices to show that the relative Čech cohomology groups
![]() $H^2(\mathfrak M(A),\mathcal Z(J),\mathbb {Z} )=0$
for all ideals
$H^2(\mathfrak M(A),\mathcal Z(J),\mathbb {Z} )=0$
for all ideals
![]() $J\subset A$
. However, due to the strong excision property for cohomology (see, e.g., [Reference Spanier20, Chapter 6, Theorem 5]), the pullback map
$J\subset A$
. However, due to the strong excision property for cohomology (see, e.g., [Reference Spanier20, Chapter 6, Theorem 5]), the pullback map
![]() $Q_J^*$
induces an isomorphism of the Čech cohomology groups
$Q_J^*$
induces an isomorphism of the Čech cohomology groups
![]() $H^2(\mathfrak M(A_J),\mathbb {Z} )\cong H^2(\mathfrak M(A),\mathcal Z(J),\,\mathbb {Z} )$
. In particular,
$H^2(\mathfrak M(A_J),\mathbb {Z} )\cong H^2(\mathfrak M(A),\mathcal Z(J),\,\mathbb {Z} )$
. In particular,
![]() $H^2(\mathfrak M(A),\mathcal Z(J),\,\mathbb {Z} )=0$
, as required.
$H^2(\mathfrak M(A),\mathcal Z(J),\,\mathbb {Z} )=0$
, as required.
4 Concluding remarks
There are some applications of Theorems 1.1 and 1.2 to operator-valued
![]() $BV(I)$
functions and to interpolating problems for
$BV(I)$
functions and to interpolating problems for
![]() $BV(I)$
maps into some complex manifolds analogous to those of [Reference Brudnyi4, Section 1.2] and [Reference Brudnyi5, Theorems 1.4, 1.6]. These results will be published elsewhere. Here, we formulate one of such results.
$BV(I)$
maps into some complex manifolds analogous to those of [Reference Brudnyi4, Section 1.2] and [Reference Brudnyi5, Theorems 1.4, 1.6]. These results will be published elsewhere. Here, we formulate one of such results.
Let
![]() $A\subset BV(I)$
be a weakly inverse-closed complex Banach function algebra, and let
$A\subset BV(I)$
be a weakly inverse-closed complex Banach function algebra, and let
![]() $L(X)$
be the Banach algebra of bounded linear operators on a complex Banach space X equipped with the operator norm. Let
$L(X)$
be the Banach algebra of bounded linear operators on a complex Banach space X equipped with the operator norm. Let
![]() $\alpha $
be either the projective cross norm
$\alpha $
be either the projective cross norm
![]() $\pi $
or the injective cross norm
$\pi $
or the injective cross norm
![]() $\varepsilon $
on the algebraic tensor product
$\varepsilon $
on the algebraic tensor product
![]() $A\otimes L(X)$
, and let
$A\otimes L(X)$
, and let
![]() $A\widehat {\otimes }_{\alpha } L(X)$
be the completion with respect to
$A\widehat {\otimes }_{\alpha } L(X)$
be the completion with respect to
![]() $\alpha $
. If
$\alpha $
. If
![]() $\alpha =\varepsilon $
, we additionally assume that the algebra A is uniform (i.e.,
$\alpha =\varepsilon $
, we additionally assume that the algebra A is uniform (i.e.,
![]() $\|a^2\|=\|a\|^2$
for all
$\|a^2\|=\|a\|^2$
for all
![]() $a\in A$
). Then
$a\in A$
). Then
![]() $A\widehat {\otimes }_{\alpha } L(X)$
is also a Banach algebra (see, e.g., [Reference Dineen, Harte and Taylor10, Section 1.3] for the references). We denote by
$A\widehat {\otimes }_{\alpha } L(X)$
is also a Banach algebra (see, e.g., [Reference Dineen, Harte and Taylor10, Section 1.3] for the references). We denote by
![]() $(A\widehat {\otimes }_{\alpha } L(X))^{-1}$
and
$(A\widehat {\otimes }_{\alpha } L(X))^{-1}$
and
![]() $\mathrm {id}\, A\widehat {\otimes }_{\alpha } L(X)=\{F\in A\widehat {\otimes }_{\alpha } L(X)\, :\, F^2=F\}$
the group of invertible elements and the set of idempotents of
$\mathrm {id}\, A\widehat {\otimes }_{\alpha } L(X)=\{F\in A\widehat {\otimes }_{\alpha } L(X)\, :\, F^2=F\}$
the group of invertible elements and the set of idempotents of
![]() $A\widehat {\otimes }_{\alpha } L(X)$
.
$A\widehat {\otimes }_{\alpha } L(X)$
.
We say that idempotents
![]() $F_1,F_2\in \mathrm {id}\, A\widehat {\otimes }_{\alpha } L(X)$
are equivalent if
$F_1,F_2\in \mathrm {id}\, A\widehat {\otimes }_{\alpha } L(X)$
are equivalent if
![]() $F_2=G^{-1}\cdot F_1\cdot G$
for some
$F_2=G^{-1}\cdot F_1\cdot G$
for some
![]() $G\in (A\widehat {\otimes }_{\alpha } L(X))^{-1}$
.
$G\in (A\widehat {\otimes }_{\alpha } L(X))^{-1}$
.
An idempotent
![]() $F\in \mathrm {id}\, A\widehat {\otimes }_{\alpha } L(X)$
is said to be locally constant if there exist idempotents
$F\in \mathrm {id}\, A\widehat {\otimes }_{\alpha } L(X)$
is said to be locally constant if there exist idempotents
![]() $p_1,\dots , p_k\in A$
with
$p_1,\dots , p_k\in A$
with
![]() $\sum _{j=1}^k p_j=1_I$
and
$\sum _{j=1}^k p_j=1_I$
and
![]() $I_1,\dots , I_k\in L(X)$
,
$I_1,\dots , I_k\in L(X)$
,
![]() $k\in \mathbb {N}$
, such that
$k\in \mathbb {N}$
, such that
 $$\begin{align*}F=\sum_{j=1}^k p_j\otimes I_j. \end{align*}$$
$$\begin{align*}F=\sum_{j=1}^k p_j\otimes I_j. \end{align*}$$
With the above notation, we have the following generalization of Theorem 1.1.
Theorem Suppose that X is isomorphic to one of the spaces: a Hilbert space,
![]() $c_0$
, or
$c_0$
, or
![]() $\ell ^p$
,
$\ell ^p$
,
![]() $1\le p\le \infty $
. Then every idempotent in
$1\le p\le \infty $
. Then every idempotent in
![]() $\mathrm {id}\, A\widehat {\otimes }_{\alpha } L(X)$
is equivalent to a locally constant idempotent.
$\mathrm {id}\, A\widehat {\otimes }_{\alpha } L(X)$
is equivalent to a locally constant idempotent.
Acknowledgment
I thank the anonymous referee for useful remarks and comments improving the presentation of the paper.



