No CrossRef data available.
Published online by Cambridge University Press: 15 May 2023
A simple polytope P is called B-rigid if its combinatorial type is determined by the cohomology ring of the moment-angle manifold 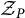 $\mathcal {Z}_P$ over P. We show that any tensor product decomposition of this cohomology ring is geometrically realized by a product decomposition of the moment-angle manifold up to equivariant diffeomorphism. As an application, we find that B-rigid polytopes are closed under products, generalizing some recent results in the toric topology literature. Algebraically, our proof establishes that the Koszul homology of a Gorenstein Stanley–Reisner ring admits a nontrivial tensor product decomposition if and only if the underlying simplicial complex decomposes as a join of full subcomplexes.
$\mathcal {Z}_P$ over P. We show that any tensor product decomposition of this cohomology ring is geometrically realized by a product decomposition of the moment-angle manifold up to equivariant diffeomorphism. As an application, we find that B-rigid polytopes are closed under products, generalizing some recent results in the toric topology literature. Algebraically, our proof establishes that the Koszul homology of a Gorenstein Stanley–Reisner ring admits a nontrivial tensor product decomposition if and only if the underlying simplicial complex decomposes as a join of full subcomplexes.
During this work, the first author was hosted by the Institute for Computational and Experimental Research in Mathematics in Providence, RI, supported by the National Science Foundation under Grant No. 1929284. The second author was hosted by the Mathematical Sciences Research Institute in Berkeley, CA, supported by the National Science Foundation under Grant No. 1928930.