In 1970, Kotzig and Rosa defined the concept of edge-magic labelings as follows. Let $G$ be a simple 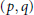$\left( p,\,q \right)$-graph (that is, a graph of order 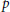$p$ and size 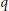$q$ without loops or multiple edges). A bijective function 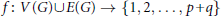$f:\,V\left( G \right)\cup E\left( G \right)\,\to \,\left\{ 1,\,2,\,.\,.\,.\,,\,p\,+\,q \right\}$ is an edge-magic labeling of $G$ if 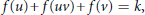$f\left( u \right)\,+\,f\left( uv \right)\,+f\left( v \right)\,=\,k$, for all 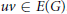$uv\,\in \,E\left( G \right)$. A graph that admits an edge-magic labeling is called an edge-magic graph, and 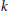$k$ is called the magic sum of the labeling. An old conjecture of Godbold and Slater states that all possible theoretical magic sums are attained for each cycle of order 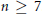$n\,\ge \,7$. Motivated by this conjecture, we prove that for all ${{n}_{0}}\,\in \,\mathbb{N}$, there exists 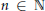$n\,\in \,\mathbb{N}$ such that the cycle 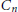${{C}_{n}}$ admits at least 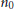${{n}_{0}}$ edge-magic labelings with at least 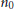${{n}_{0}}$ mutually distinct magic sums. We do this by providing a lower bound for the number of magic sums of the cycle 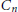${{C}_{n}}$, depending on the sum of the exponents of the odd primes appearing in the prime factorization of $n$.