Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T14:42:44.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Power Series Rings Over Prüfer v-multiplication Domains. II

Published online by Cambridge University Press:  20 November 2018

Gyu Whan Chang
Gyu Whan Chang*
Affiliation:
Department of Mathematics Education, Incheon National University, Incheon 22012, Korea e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $D$ be an integral domain, 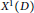${{X}^{1}}\left( D \right)$ be the set of height-one prime ideals of $D$, 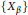$\left\{ {{X}_{\beta }} \right\}$ and 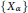$\left\{ {{X}_{\alpha }} \right\}$ be two disjoint nonempty sets of indeterminates over $D$, $D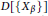\left[ \left\{ {{X}_{\beta }} \right\} \right]$ be the polynomial ring over $D$, and 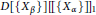$D\left[ \left\{ {{X}_{\beta }} \right\} \right]{{\left[\!\left[ \left\{ {{X}_{\alpha }} \right\} \right]\!\right]}_{1}}$ be the first type power series ring over 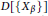$D\left[ \left\{ {{X}_{\beta }} \right\} \right]$. Assume that $D$ is a Prüfer $v$-multiplication domain $\left( \text{P}v\text{MD} \right)$ in which each proper integral $t$-ideal has only finitely many minimal prime ideals (e.g., $t$-$\t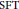ext{SFT}$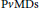$\text{P}v\text{MDs}$, valuation domains, rings of Krull type). Among other things, we show that if 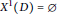${{X}^{1}}\left( D \right)\,=\,\phi$ or 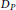${{D}_{p}}$ is a 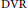$\text{DVR}$ for all 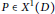$P\,\in \,{{X}^{1}}\left( D \right)$, then $D\left[ \left\{ {{X}_{\beta }} \right\} \right]{{\left[\!\left[ \left\{ {{X}_{\alpha }} \right\} \right]\!\right]}_{1D-\left\{ 0 \right\}}}$ is a Krull domain. We also prove that if $D$ is a $t$-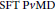$\text{SFT}\text{P}v\text{MD}$, then the complete integral closure of $D$ is a Krull domain and 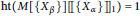$\text{ht}\left( M\left[ \left\{ {{X}_{\beta }} \right\} \right]{{\left[\!\left[ \left\{ {{X}_{\alpha }} \right\} \right]\!\right]}_{1}} \right)\,=\,1$ for every height-one maximal $t$-ideal 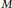$M$ of $D$.

Keywords

13A1513F0513F25Krull domainPvMDmultiplicatively closed set of idealspower series ring
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 1 , 01 March 2017 , pp. 63 - 76
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Anderson, D. D., D. E Anderson, and Zafrullah, M., The ring D + XDg [X] and t-splitting sets. In: Commutative algebra, Arab J. Sci. Eng. Sect. C Theme Issues 26(2001), 3–16.Google Scholar
[2] Anderson, D. D., Chang, G. W., and Zafrullah, M., Integral domains of finite t-character. J. Algebra 396(2013), 169–183. http://dx.doi.Org/10.1016/j.jalgebra.2013.08.014 Google Scholar
[3] Anderson, D. D., Kang, B. G., and Park, M. H., Anti-Archimedean rings and power series rings. Comm. Algebra 26(1998), no. 10 ,3223-3238. http://dx.doi.Org/10.1080/00927879808826338 Google Scholar
[4] Arnold, J. T., Power series rings over Prtifer domains. Pacific J. Math. 44(1973), 1–11. http://dx.doi.Org/10.2140/pjm.1973.44.1 Google Scholar
[5] Arnold, J. T., Power series rings with finite Krull dimension. Indiana Univ. Math. J. 31(1982), no. 6, 897–911. http://dx.doi.Org/10.1512/iumj.1982.31.31061 Google Scholar
[6] Arnold, J. T. and Brewer, J. W., On flat overrings, ideal transforms and generalized transforms of a commutative ring. J. Algebra 18(1971), 254–263. http://dx.doi.Org/10.1016/0021-8693(71)9OO58-5 Google Scholar
[7] Chang, G. W., Spectral localizing systems that are t-splitting multiplicative sets of ideals. J. Korean Math. Soc. 44(2007), 863–872. http://dx.doi.Org/10.4134/JKMS.2007.44.4.863 Google Scholar
[8] Chang, G. W., Power series rings over Priifer v-multiplication domains. J. Korean Math. Soc. 53(2016), no. 2, 447–459. http://dx.doi.Org/10.4134/JKMS.2016.53.2.447 Google Scholar
[9] Chang, G. W. and Oh, D. Y., The rings D((X))i and D﹛﹛X﹜﹜;. J. Algebra Appl. 12(2013), no. 2, 1250147. http://dx.doi.Org/10.1142/S0219498812 501472 Google Scholar
[10] Decruyenaere, E. and Jespers, E., Priifer domains and graded rings. J. Algebra 150(1992), no. 2, 308–320. http://dx.doi.Org/10.1016/S0021-8693(05)80034-1 Google Scholar
[11] Dobbs, D., Houston, E., Lucas, T., and Zafrullah, M., t-linked overrings and Priifer v-multiplication domains. Comm. Algebra 17(1989), no. 11, 2835–2852. http://dx.doi.org/10.1080/0092787890882387.Google Scholar
[12] El Baghdadi, S., On a class of Priifer v-multiplication domains. Comm. Algebra 30(2002), no. 8, 3723-3724. http://dx.doi.Org/10.1081/ACB-120005815 Google Scholar
[13] El Baghdadi, S. and Kim, H., Generalized Krull semigroup rings. Comm. Algebra 44(2016), no. 4, 1783–1794. http://dx.doi.Org/10.1080/00927872.2015.1027378 Google Scholar
[14] Fontana, M., Gabelli, S., and Houston, E., UMT-domains and domains with Priifer integral closure. Comm. Algebra 26(1998), 1017–1039. http://dx.doi.Org/10.1080/00927879808826181 Google Scholar
[15] Fontana, M., Huckaba, J. A., and Papick, I. J., Priifer domains. Monographs and Textbooks in Pure and Applied Math., 203, Marcel Dekker, New York, 1997.Google Scholar
[16] Fossum, R. M., The divisor class group of a Krull domain. Springer-Verlag, New York-Heidelberg, 1973.Google Scholar
[17] Gabelli, S., Generalized Dedekind domains. In: Multiplicative ideal theory in commutative algebra, Springer, New York, 2006, pp. 189–206. http://dx.doi.Org/10.1007/978-0-387-36717-0J2 Google Scholar
[18] Gilmer, R., Power series rings over a Krull domain. Pacific J. Math. 29(1969), 543–549. http://dx.doi.Org/10.2140/pjm.1969.29.543 Google Scholar
[19] Gilmer, R., Multiplicative ideal theory. Pure and Applied Mathematics, 12, Marcel Dekker, New York, 1972.Google Scholar
[20] Griffin, M., Some results on v-multiplication rings. Cana Math d. J. 19(1967), 710–722. http://dx.doi.Org/10.4153/CJM-1967-065-8 Google Scholar
[21] Griffin, M., Rings ofKrull type. J. Reine Angew. Math. 229(1968), 1–27.Google Scholar
[22] Kang, B. G., Prüfer v-multiplication domains and the ring R[X]Ny. J. Algebra 123(1989), no. 1, 151–170. http://dx.doi.Org/10.1 01 6/0021-8693(89)90040-9 Google Scholar
[23] Kang, B. G. and Park, M. H., On Mockor's question. J. Algebra 216(1999), 481–510. http://dx.doi.Org/10.1006/jabr.1 998.7785 Google Scholar
[24] Kang, B. G., A note on t-SFT-rings. Comm. Algebra 34(2006), no. 9, 3153–3165. http://dx.doi.Org/10.1080/00927870600639476 Google Scholar
[25] Mott, J. L., On the complete integral closure of an integral domain ofKrull type. Math. Ann. 173(1967), 238–240. http://dx.doi.Org/10.1007/BF01361714 Google Scholar
[26] Mott, J. L. and Zafrullah, M., On Priifer v-multiplication domains. Manuscripta Math. 35(1981), 1–26. http://dx.doi.Org/10.1007/BF011 68446 Google Scholar
[27] Ohm, J., Some counterexamples related to integral closure in D[[X]]. Trans. Amer. Math. Soc. 122(1966), 321–333.Google Scholar
[28] Paran, E. and Temkin, M., Power series over generalized Krull domains. J. Algebra 323(2010), no. 2, 546–550. http://dx.doi.Org/10.1016/j.jalgebra.2009.08.011 Google Scholar
[29] Popescu, N., On a class of Priifer domains. Rev. Roumaine Math. Pures Appl. 29(1984), 777–786.Google Scholar
[30] Samuel, P., On unique factorization domains. Illinois J. Math. 5(1961), 1–17.Google Scholar