Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-24T02:13:41.006Z Has data issue: false hasContentIssue false
  • English
  • Français

Power Residue Criteria for Quadratic Units and the Negative Pell Equation

Published online by Cambridge University Press:  20 November 2018

Tommy Bülow
Tommy Bülow*
Affiliation:
Department of Mathematics, University of Copenhagen, DK-2100 Copenhagen, Denmark, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 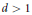$d\,>\,1$ be a square-free integer. Power residue criteria for the fundamental unit 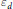${{\varepsilon }_{d}}$ of the real quadratic fields 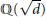$\mathbb{Q}(\sqrt{d})$ modulo a prime 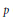$p$ (for certain 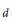$d$ and 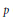$p$) are proved by means of class field theory. These results will then be interpreted as criteria for the solvability of the negative Pell equation 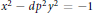${{x}^{2}}\,-\,d{{p}^{2}}{{y}^{2}}\,=\,-1$. The most important solvability criterion deals with all 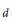$d$ for which 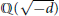$\mathbb{Q}(\sqrt{-d})$ has an elementary abelian 2-class group and 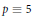$p\,\equiv \,5$ (mod 8) or 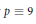$p\,\equiv \,9$ (mod 16).

Keywords

11R1111R27
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 1 , 01 March 2003 , pp. 39 - 53
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Cassels, J. W. S. and Fröhlich, A., Algebraic Number Theory. Thompson, Washington D.C, 1967.Google Scholar
[2] Dirichlet, P. G. L., Einige neue Sätze über unbestimmte Gleichungen. Gesammelte Werke, Chelsea, New York, 219–236.Google Scholar
[3] Furuta, Y., Norm of Units of Quadratic Fields. J. Math. Soc. Japan 11 (1959), 139–145.Google Scholar
[4] Halter-Koch, F., Konstruktion von Klassenkörpern und Potenzrestkriterien für quadratische Einheiten. Manuscripta Math 54 (1986), 453–492.Google Scholar
[5] Hasse, H., Vorlesungen über Klassenkörpertheorie. Physica-Verlag, Würzburg, 1967.Google Scholar
[6] Hecke, E., Lectures on the Theory of Algebraic Numbers. Springer-Verlag, 1981.Google Scholar
[7] Jensen, Chr. U., On the Solvability of a Certain Class of non-Pellian Equations. Math. Scand. 10 (1962), 71–84.Google Scholar
[8] Jensen, Chr. U., On the Diophantine Equation ξ2 − 2m2η2 = −1. Math. Scand. 11 (1962), 58–62.Google Scholar
[9] Perrot, J., Sur l'equation t2 − Dy2 = −1. J. Reine Angew.Math. 102 (1888), 185–223.Google Scholar
[10] Rédei, L., Bedingtes Artinsymbol mit Anwendungen in der Klassenkörpertheorie. Acta Math. Sci. Hung. 4 (1953), 1–29.Google Scholar
[11] Rédei, L., Die 2-Ringklassengruppe des quadratischen Zahlkörpers und die Theorie der Pellschen Gleichung. Acta Math. Sci. Hung. 4 (1953), 31–87.Google Scholar
[12] Rédei, L. and Reichardt, H., Die Anzahl der durch 4 teilbaren Invarianten der Klassengruppe eines beliebigen quadratischen Zahlkörbers. J. Reine Angew.Math. 170 (1934), 69–74.Google Scholar
[13] Scholz, A., Über die Lo¨sbarkeit der Gleichung t2 − Du2 = −4. Math. Zeitschrift 39 (1935), 95–111.Google Scholar