Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-05T19:30:24.975Z Has data issue: false hasContentIssue false
  • English
  • Français

Positive Definite Distributions and Subspaces of L_p With Applications to Stable Processes

Published online by Cambridge University Press:  20 November 2018

Alexander Koldobsky
Alexander Koldobsky*
Affiliation:
Division of Mathematics and Statistics University of Texas at San Antonio San Antonio, Texas 78249 U.S.A., email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We define embedding of an $n$-dimensional normed space into ${{L}_{-p}},\,0\,<\,p\,<\,n$ by extending analytically with respect to 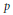$p$ the corresponding property of the classical ${{L}_{p}}$-spaces. The well-known connection between embeddings into ${{L}_{p}}$ and positive definite functions is extended to the case of negative 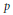$p$ by showing that a normed space embeds in 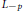${{L}_{-p}}$ if and only if 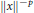$\parallel x{{\parallel }^{-p}}$ is a positive definite distribution. We show that the technique of embedding in 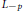${{L}_{-p}}$ can be applied to stable processes in some situations where standard methods do not work. As an example, we prove inequalities of correlation type for the expectations of norms of stable vectors. In particular, for every 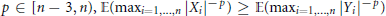$P\in [n-3,n),\mathbb{E}({{\max }_{i=1,...,n}}{{\left| {{X}_{i}} \right|}^{-p}})\ge \mathbb{E}({{\max }_{i=1,...,n}}{{\left| {{Y}_{i}} \right|}^{-p}})$, where 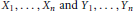${{X}_{1}},...,{{X}_{n}}\,\text{and}\,{{Y}_{1}},...,{{Y}_{n}}$ are jointly 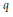$q$-stable symmetric random variables, 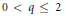$0\,<\,q\,\le \,2$, so that, for some 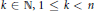$k\,\in \,\mathbb{N},\,1\,\le \,k\,<\,n$, the vectors 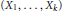$\left( {{X}_{1}},\,.\,.\,.\,,\,{{X}_{k}} \right)$ and 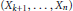$\left( {{X}_{k+1}},\,.\,.\,.\,,{{X}_{n}} \right)$ have the same distributions as 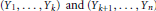$({{Y}_{1}},...,{{Y}_{k}})\,\,\text{and}\,\,({{Y}_{k+1}},...,{{Y}_{n}})$, respectively, but 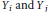${{Y}_{i}}\,\text{and}\,{{Y}_{j}}$ are independent for every choice of 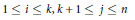$1\,\le \,i\,\le \,k,\,k\,+\,1\,\le \,j\,\le \,n$.

Keywords

42A8246B0446F1260E07
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 3 , 01 September 1999 , pp. 344 - 353
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Bretagnolle, J., Dacunha-Castelle, D. and Krivine, J. L., Lois stables et espaces Lp . Ann. Inst. H. Poincaré Probab. Statist. 2 (1966), 231–259.Google Scholar
[2] Clarkson, J. A., Uniformly convex spaces. Trans. Amer.Math. Soc. 40 (1936), 396–414.Google Scholar
[3] Ferguson, T. S., A representation of the symmetric bivariate Cauchy distributions. Ann. Math. Stat. 33 (1962), 1256–1266.Google Scholar
[4] Gelfand, I. M. and Shilov, G. E., Generalized functions 1. Properties and operations. Academic Press, New York, 1964.Google Scholar
[5] Gelfand, I. M. and Vilenkin, N. Ya., Generalized functions 4. Applications of harmonic analysis. Academic Press, New York, 1964.Google Scholar
[6] Herz, C., A class of negative definite functions. Proc. Amer.Math. Soc. 14 (1963), 670–676.Google Scholar
[7] Koldobsky, A., Schoenberg's problem on positive definite functions. Algebra and Analysis 3 (1991), 78–85 (English translation in St. Petersburg Math. J. 3 (1992), 563–570).Google Scholar
[8] Koldobsky, A., Generalized Lévy representation of norms and isometric embeddings into Lp-spaces. Ann. Inst. H. Poincaré Sér. B 28 (1992), 335–353,Google Scholar
[9] Koldobsky, A., Characterization of measures by potentials. J. Theoret. Probab. 7 (1994), 135–145.Google Scholar
[10] Koldobsky, A., Positive definite functions, stable measures, and isometries on Banach spaces. Lecture Notes in Pure and Appl. Math. 175 (1995), 275–290.Google Scholar
[11] Koldobsky, A., Inverse formula for the Blaschke-Lévy representation. Houston J. Math. 23 (1997), 95–107.Google Scholar
[12] Koldobsky, A., An application of the Fourier transform to sections of star bodies. Israel J.Math. 106 (1998), 157–164.Google Scholar
[13] Koldobsky, A., Intersection bodies in R4. Adv. Math. 136 (1998), 1–14.Google Scholar
[14] Lévy, P., Théorie de l’addition de variable aléatoires. Gauthier-Villars, Paris, 1937.Google Scholar
[15] Misiewicz, J., Positive definite functions on 1. Statist. Probab. Lett. 8 (1989), 255–260.Google Scholar
[16] Misiewicz, J., Sub-stable and pseudo-isotropic processes—connections with the geometry of subspaces of L*-spaces. Dissertationes Math. 358(1996).Google Scholar
[17] Schechtman, G., Schlumprecht, T. and Zinn, J., On the Gaussian measure of the intersection of symmetric convex sets. Preprint.Google Scholar
[18] Schoenberg, I. J., Metric spaces and positive definite functions. Trans. Amer.Math. Soc. 44 (1938), 522–536.Google Scholar
[19] Zolotarev, V. M., One-dimensional stable distributions. Amer. Math. Soc., Providence, RI, 1986.Google Scholar