Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-04-25T19:26:46.710Z Has data issue: false hasContentIssue false
  • English
  • Français

Poncelet’s closure theorem and the embedded topology of conic-line arrangements

Part of: Birational geometry Curves Low-dimensional topology

Published online by Cambridge University Press:  25 November 2024

Shinzo Bannai Open the ORCID record for Shinzo Bannai [Opens in a new window] ,
Ryosuke Masuya ,
Taketo Shirane Open the ORCID record for Taketo Shirane [Opens in a new window] ,
Hiro-o Tokunaga  and
Emiko Yorisaki
Shinzo Bannai*
Affiliation:
Department of Applied Mathematics, Faculty of Science, Okayama University of Science, 1-1 Ridai-cho, Kita-ku, Okayama 700-0005, Japan
Ryosuke Masuya
Affiliation:
Department of Mathematical Sciences, Graduate School of Science, Tokyo Metropolitan University, 1-1 Minami-Ohsawa, Hachiohji 192-0397, Japan e-mail: [email protected] [email protected] [email protected]
Taketo Shirane
Affiliation:
Department of Mathematical Sciences, Graduate School of Science, Tokyo Metropolitan University, 1-1 Minami-Ohsawa, Hachiohji 192-0397, Japan e-mail: [email protected] [email protected] [email protected]
Hiro-o Tokunaga
Affiliation:
Department of Mathematical Sciences, Graduate School of Science, Tokyo Metropolitan University, 1-1 Minami-Ohsawa, Hachiohji 192-0397, Japan e-mail: [email protected] [email protected] [email protected]
Emiko Yorisaki
Affiliation:
Department of Mathematical Science, Faculty of Science and Technology, Tokushima University, 2-1 Minamijyousanjima-cho, Tokushima 770-8506, Japan e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In the study of plane curves, one of the problems is to classify the embedded topology of plane curves in the complex projective plane that have a given fixed combinatorial type, where the combinatorial type of a plane curve is data equivalent to the embedded topology in its tubular neighborhood. A pair of plane curves with the same combinatorial type but distinct embedded topology is called a Zariski pair. In this paper, we consider Zariski pairs consisting of conic-line arrangements that arise from Poncelet’s closure theorem. We study unramified double covers of the union of two conics that are induced by a 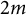$2m$-sided Poncelet transverse. As an application, we show the existence of families of Zariski pairs of degree 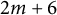$2m+6$ for 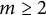$m\geq 2$ that consist of reducible curves having two conics and 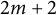$2m+2$ lines as irreducible components.

Keywords

conic-line arrangementsembedded topologyPoncelet’s closure theoremZariski pairssplitting invariants

MSC classification

Primary: 14E20: Coverings 14H30: Coverings, fundamental group 14H50: Plane and space curves 57M10: Covering spaces
Type
Article
Information
Canadian Mathematical Bulletin , Volume 68 , Issue 1 , March 2025 , pp. 109 - 123
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The first author was partially supported by JSPS KAKENHI Grant Numbers JP18K03263, JP23K03042. The third author was partially supported by JSPS KAKENHI Grant Number JP21K03182. The fourth author was partially supported by JSPS KAKENHI Grant Number JP20K03561, JP24K06673.

References

Bartolo, E. A., Sur les couples de Zariski. J. Algebraic Geom. 3(1994), no. 2, 223–247.Google Scholar
Bartolo, E. A., Bannai, S., Shirane, T. and Tokunaga, H., Torsion divisors of plane curves and Zariski pairs. St. Petersburg Math. J. 34(2023), 721–736.CrossRefGoogle Scholar
Bartolo, E. A., Bannai, S., Shirane, T. and Tokunaga, H., Torsion divisors of plane curves with maximal flexes and Zariski pairs. Math. Nachr. 296(2023), no. 6, 2214–2235.CrossRefGoogle Scholar
Bartolo, E. A., Ruber, J. C., Cogolludo-Agustín, J. I. and Buzunáriz, M. M., Topology and combinatorics of real line arrangements. Compos. Math. 141(2005), no. 6, 1578–1588.CrossRefGoogle Scholar
Bartolo, E. A., Cogolludo, J. I. and Tokunaga, H., A survey on Zariski pairs . In Algebraic geometry in East Asia—Hanoi 2005, Adv. Stud. Pure Math., Vol. 50, Math. Soc. Japan, Tokyo, 2008, 1–100.Google Scholar
Bannai, S., A note on splitting curves of plane quartics and multi-sections of rational elliptic surfaces. Topology Appl., 202(2016), 428–439.CrossRefGoogle Scholar
Bannai, S., Shirane, T. and Tokunaga, H., Arithmetic of double covers and its application to the topology of plane curves. Submitted.Google Scholar
Bannai, S. and Tokunaga, H., Zariski tuples for a smooth cubic and its tangent lines. Proc. Japan Acad. Ser. A Math. Sci. 96(2020), no. 2, 18–21.CrossRefGoogle Scholar
Barth, W. and Bauer, T., Poncelet theorems. Expo. Math. 14(1996), no. 2, 125–144.Google Scholar
Griffiths, P. and Harris, J., On Cayley’s explicit solution to Poncelet’s porism. Enseign. Math. (2) 24(1978), no. 1–2, 31–40.Google Scholar
Harris, J., Theta-characteristics on algebraic curves. Trans. Amer. Math. Soc. 271(1982), no. 2, 611–638.CrossRefGoogle Scholar
Masuya, R., Geometry of weak-bitangent lines to quartic curves and sections on certain rational elliptic surfaces. Hiroshima Math. J. 54(2024), no. 1, 1–35.CrossRefGoogle Scholar
Nazir, S. and Yoshinaga, M., On the connectivity of the realization spaces of line arrangements. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 11(2012), no. 4, 921–937.Google Scholar
Oka, M., Zariski pairs on sextics. II . In Singularity theory, World Sci. Publ., Hackensack, NJ, 2007, 837–863.CrossRefGoogle Scholar
Poncelet, J.-V., Traité des propriétés projectives des figures, Paris, 1822.Google Scholar
Tokunaga, H., Sections of elliptic surfaces and Zariski pairs for conic-line arrangements via dihedral covers. J. Math. Soc. Japan 66(2014), no. 2, 613–640.CrossRefGoogle Scholar
Zariski, O., On the problem of existence of algebraic functions of two variables possessing a given branch curve. Amer. J. Math. 51(1929), no. 2, 305–328.CrossRefGoogle Scholar