Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T01:41:29.209Z Has data issue: false hasContentIssue false
  • English
  • Français

Polynomials for Kloosterman Sums

Published online by Cambridge University Press:  20 November 2018

S. Gurak
S. Gurak*
Affiliation:
University of San Diego, San Diego, CA 92110, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Fix an integer 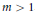$m>1$, and set 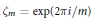${{\zeta }_{m}}=\exp \left( 2\pi i/m \right)$. Let 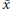$\bar{x}$ denote the multiplicative inverse of 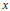$x$ modulo 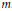$m$. The Kloosterman sums 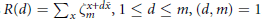$R\left( d \right)=\sum\limits_{x}{\zeta _{m}^{x+d\bar{x}}},1\le d\le m,\left( d,m \right)=1$, satisfy the polynomial

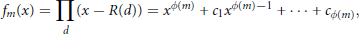$${{f}_{m}}\left( x \right)=\underset{d}{\mathop{\prod }}\,\left( x-R\left( d \right) \right)={{x}^{\phi \left( m \right)}}+{{c}_{1}}{{x}^{\phi \left( m \right)-1}}+\cdot \cdot \cdot +{{c}_{\phi \left( m \right)}},$$

where the sum and product are taken over a complete system of reduced residues modulo 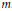$m$. Here we give a natural factorization of 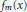${{f}_{m}}\left( x \right)$, namely,

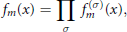$${{f}_{m}}\left( x \right)=\underset{\sigma }{\mathop{\prod }}\,f_{m}^{\left( \sigma \right)}\left( x \right),$$

where 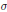$\sigma$ runs through the square classes of the group 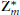$Z_{m}^{*}$ of reduced residues modulo 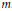$m$. Questions concerning the explicit determination of the factors 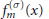$f_{m}^{\left( \sigma \right)}\left( x \right)$ (or at least their beginning coefficients), their reducibility over the rational field 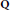$\text{Q}$ and duplication among the factors are studied. The treatment is similar to what has been done for period polynomials for finite fields.

Keywords

11L0511T24
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 1 , 01 March 2007 , pp. 71 - 84
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Berndt, B. C., Evans, R. J. and Williams, K. S., Gauss and Jacobi Sums. Canadian Mathematical Society Series of Monographs and Advanced Texts. Wiley-Interscience, New York, 1998.Google Scholar
[2] Borevich, Z. and Shafarevich, I., Number Theory. Pure and Applied Mathematics 20, Academic Press, New York, 1966.Google Scholar
[3] Gaal, L., Classical Galois Theory with Examples. Chelsea, New York, 1973.Google Scholar
[4] Gupta, S. and Zagier, D., On the coefficients of the minimal polynomial of Gaussian periods. Math. Comp. 60(1993), 385–398.Google Scholar
[5] Gurak, S., Minimal polynomials for circular numbers. Pacific J. Math 112(1984), no. 2, 313–331.Google Scholar
[6] Gurak, S., Factors of period polynomials for finite fields. I. In: The Rademacher Legacy toMathematics, Contemp. Math. 166, American Mathematical Society, Providence, RI, 1994), pp. 309–333.Google Scholar
[7] Gurak, S., On the minimal polynomials for certain Gauss periods over finite fields. In: Finite Fields and their Applications, LondonMath. Soc. Lecture Note Ser. 233, Cambridge, Cambridge University Press, 1996, pp. 85–96.Google Scholar
[8] Gurak, S., Minimal polynomials for Gauss periods with f = 2 . Acta Arith. 121(2006), 233–257.Google Scholar
[9] Iwaniec, H., Topics in classical automorphic forms. Graduate Studies in Mathematics 17, American Mathematical Society, Providence, RI, 1997.Google Scholar
[10] Lehmer, D., On the cubes of Kloosterman sums. Acta Arith. 6(1960), 15–22.Google Scholar
[11] Myerson, G., Period polynomials and Gauss sums for finite fields. Acta Arith. 39(1981), no. 3, 251–264.Google Scholar
[12] Salie, H., Über die Kloostermanschen Summen S(u, v; q) . Math Z. 34(1932), no. 1, 91–109.Google Scholar
[13] Sarnak, P., Some applications of modular forms. Cambridge Tracts in Mathematics 99, Cambridge University Press, Cambridge, 1990.Google Scholar