Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T07:31:02.468Z Has data issue: false hasContentIssue false
  • English
  • Français

Poincaré Inequalities and Neumann Problems for the p-Laplacian

Published online by Cambridge University Press:  20 November 2018

David Cruz-Uribe ,
Scott Rodney  and
Emily Rosta
David Cruz-Uribe
Affiliation:
Department of Mathematics, University of Alabama, Tuscaloosa, Alabama 35487, USA, e-mail : [email protected]
Scott Rodney
Affiliation:
Dept. of Mathematics, Physics and Geology, Cape Breton University, Sydney, Nova Scotia B1Y3V3, e-mail : [email protected], [email protected]
Emily Rosta
Affiliation:
Dept. of Mathematics, Physics and Geology, Cape Breton University, Sydney, Nova Scotia B1Y3V3, e-mail : [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove an equivalence between weighted Poincaré inequalities and the existence of weak solutions to a Neumann problem related to a degenerate 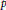$p$-Laplacian. The Poincaré inequalities are formulated in the context of degenerate Sobolev spaces defined in terms of a quadratic form, and the associated matrix is the source of the degeneracy in the 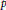$p$-Laplacian.

Keywords

30C6535B6535J7042B3542B3746E35degenerate Sobolev spacep-LaplacianPoincaré inequalities
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 4 , 01 December 2018 , pp. 738 - 753
Copyright
Copyright © Canadian Mathematical Society 2018

References

[CW] Chanillo, S. and Wheeden, R. L., Weighted Poincaré and Sobolev inequalities and estimates for weighted Peano maximal functions. Amer. J. Math. 107 (1985), no. 5, 1191-1226. http://dx.doi.org/10.2307/2374351Google Scholar
[C] Chua, S.-K., Weighted Sobolev inequalities on domains satisfying the chain condition. Proc. Amer. Math. Soc. 117 (1993), 449–457. http://dx.doi.Org/10.2307/2159182Google Scholar
[CRW] Chua, S.-K., Rodney, S., and Wheeden, R. L., A compact embedding theorem for generalized Sobolev spaces. Pacific J. Math. 265 (2013), no. 1,17-57. http://dx.doi.org/10.2140/pjm.2013.265.17Google Scholar
[CU] Cruz-Uribe, D., Two weight inequalities for fractional integral operators and commutators. In: Advanced courses of mathematical analysis VI, World Scientific, Hackensack, NJ, 2017, pp. 25–85.Google Scholar
[CIM] Cruz-Uribe, D., Isralowitz, J., and Moen, K., Two weight bump conditions for matrix weights. 2017. arxiv:1 710.03397Google Scholar
[CMP] Cruz-Uribe, D., Martell, J. M., and Perez, C., Weights, extrapolation and the theory of Rubio de Francia. Operator Theory: Advances and Applications, 215, Birkhâuser/Springer Basel AG, Basel, 2011. http://dx.doi.org/10.1007/978-3-0348-0072-3Google Scholar
[CMN] Cruz-Uribe, D., Moen, K., and Naibo, V., Regularity of solutions to degenerate p-Laplacian equations. J. Math Anal. Appl. 401 (2013), no. 1, 458-478. http://dx.doi.Org/10.1016/j.jmaa.2O12.12.023Google Scholar
[CMR] Cruz-Uribe, D., Moen, K., and Rodney, S., Matrix A.p weights, degenerate Sobolev spaces and mappings of finite distortion. J. Geom. Anal. 26 (2016), no. 4, 2797-2830. http://dx.doi.Org/10.1007/s12220-015-9649-8Google Scholar
[DRS] Diening, L., Ruzicka, M., and Schumacher, K., A decomposition technique for John domains. Ann. Acad. Sci. Fenn. Math. 35 (2010), 87–114. http://dx.doi.org/10.5186/aasfm.2010.3506Google Scholar
[MDJ] Dinca, G., Jebelean, P., and Mawhin, J., Variational and topological methods for Dirichlet problems with p-Laplacian. Port. Math. 58 (2001), 339–378.Google Scholar
[DUO] Duoandikoetxea, J., Fourier analysis. Graduate Studies in Mathematics, 29, American Mathematical Society, Providence, RI, 2001.Google Scholar
[FKS] Fabes, E. B., Kenig, C. E., and Serapioni, R. P., The local regularity of solutions of degenerate elliptic equations. Comm. Partial Differential Equations 7 (1982), 77–116. http://dx.doi.Org/10.1080/03605308208820218Google Scholar
[GT] Gilbarg, D. and Trudinger, N. S., Elliptic partial differential equations of second order. Grundlehren der Mathematischen Wissenschaften, 224, Springer-Verlag, Berlin-New York, 1977.Google Scholar
[L] Lindqvist, P., Notes on the p-Laplace equation. Report. Department of Mathematics and Statistics, 102, University of Jyvâskylâ, Jyvâskylâ, 2006. https://folk.ntnu.no/lqvist/p-laplace.pdfGoogle Scholar
[M] Modica, G., Quasiminima of some degenerate functionals. Ann. Mat. Pura Appl. (4) 142 (1985), 121–143. http://dx.doi.org/10.1007/BF01766591Google Scholar
[MR] Monticelli, D. D. and Rodney, S., Existence and spectral theory for weak solutions of Neumann and Dirichlet problems for linear degenerate elliptic operators with rough coefficients. J. Differential Equations 259 (2015), no. 8, 4009-4044. http://dx.doi.Org/10.1016/j.jde.2015.05.018Google Scholar
[MRW1] Monticelli, D. D., Rodney, S., and Wheeden, R. L., Boundedness of weak solutions of degenerate quasilinear equations with rough coefficients. Differential Integral Equations 25 (2012), no. 1-2, 143-200.Google Scholar
[MRW2] Monticelli, D. D., Rodney, S., and Wheeden, R. L., Harnack's inequality and Holder continuity for weak solutions of degenerate quasilinear equations with rough coefficients. Nonlinear Anal. 126 (2015), 69–114. http://dx.doi.Org/10.1016/j.na.2015.05.02 9Google Scholar
[P] Pingen, M., Regularity results for degenerate elliptic systems. Ann. Inst. H. Poincaré Anal. Non Linéaire 25 (2008), no. 2,369-380. http://dx.doi.Org/10.1016/j.anihpc.2007.02.008Google Scholar
[RS] Ron, A. and Shen, Z., Frames and stable bases for shift-invariant subspaces ofL2(R'1 ). Canad. J. Math. 47 (1995), no. 5, 1051-1094. http://dx.doi.org/10.4153/CJM-1995-056-1Google Scholar
[R] Roudenko, S., Matrix-weighted Besov spaces. Trans. Amer. Math. Soc. 355 (2003), no. 1, 273-314. http://dx.doi.Org/10.1090/S0002-9947-02-03096-9Google Scholar
[SW1] Sawyer, E. T. and Wheeden, R. L., Holder continuity of weak solutions to subelliptic equations with rough coefficients. Mem. Amer. Math. Soc. 180 (2006), no. 847. http://dx.doi.Org/10.1090/memo/0847Google Scholar
[SW2] Sawyer, E. T. and Wheeden, R. L., Degenerate Sobolev spaces and regularity of subelliptic equations. Trans. Amer. Math. Soc. 362 (2010), no. 4, 1869-1906. http://dx.doi.org/10.1090/S0002-9947-09-04756-4Google Scholar
[S] Showalter, R. E., Monotone Operators in Banach spaces and nonlinear partial differential equations. Math. Surveys and Monographs, 49, American Mathematical Society, Providence, RI, 1997.Google Scholar