Hostname: page-component-6bf8c574d5-qdpjg Total loading time: 0 Render date: 2025-02-19T20:53:25.164Z Has data issue: false hasContentIssue false
  • English
  • Français

Plane Quartic Twists of X(5, 3)

Published online by Cambridge University Press:  20 November 2018

Julio Fernández ,
Josep González  and
Joan-C. Lario
Julio Fernández
Affiliation:
Facultat de Matemàtiques i Estadística, Universitat Politècnica de Catalunya, Pau Gargallo 5, 08028 Barcelona, Spain e-mail: [email protected]@[email protected]
Josep González
Affiliation:
Facultat de Matemàtiques i Estadística, Universitat Politècnica de Catalunya, Pau Gargallo 5, 08028 Barcelona, Spain e-mail: [email protected]@[email protected]
Joan-C. Lario
Affiliation:
Facultat de Matemàtiques i Estadística, Universitat Politècnica de Catalunya, Pau Gargallo 5, 08028 Barcelona, Spain e-mail: [email protected]@[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given an odd surjective Galois representation 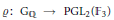$\varrho :{{\text{G}}_{\mathbb{Q}}}\to \text{PG}{{\text{L}}_{2}}\left( {{\mathbb{F}}_{3}} \right)$ and a positive integer 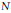$N$, there exists a twisted modular curve 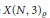$X{{\left( N,3 \right)}_{\varrho }}$ defined over 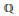$\mathbb{Q}$ whose rational points classify the quadratic 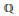$\mathbb{Q}$-curves of degree 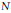$N$ realizing 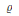$\varrho$. This paper gives a method to provide an explicit plane quartic model for this curve in the genus-three case 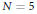$N=5$.

Keywords

11F0311F8014G05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 2 , 01 June 2007 , pp. 196 - 205
Copyright
Copyright © Canadian Mathematical Society 2007

References

[BGGP] Baker, M., González, E., González, J., and Poonen, B., Finiteness results for modular curves of genus at least 2 . Amer. J. Math. 127(2005), no. 6, 1325–1387.Google Scholar
[Cre97] Cremona, J. E., Algorithms for Modular Elliptic Curves. Second edition. Cambridge University Press, Cambridge, 1997.Google Scholar
[Fer03] Fernández, J., Elliptic Realization of Galois Representations. Ph.D. thesis, Universitat Politècnica de Catalunya, 2003.Google Scholar
[Fer04] Fernández, J., A moduli approach to quadratic ℚ-curves realizing projective mod p Galois representations. 2004. Preprint available at http://www.math.leidenuniv.nl/gtem.Google Scholar
[FLR02] Fernández, J., Lario, J.-C., and Rio, A., Octahedral Galois representations arising from ℚ-curves of degree 2 . Canad. J. Math. 54(2002), no. 6, 1202–1228.Google Scholar
[GL98] González, J. and Lario, J.-C., Rational and elliptic parametrizations of ℝ-curves. J. Number Theory, 72(1998), no. 1, 13–31.Google Scholar
[KM88] Kenku, M. A. and Momose, F., Automorphism groups of the modular curves X 0(N) . Compositio Math. 65(1988), no. 1, 51–80.Google Scholar
[Lig77] Ligozat, G., Courbes modulaires de niveau 11 . In: Modular Functions of One Variable. Lecture Notes in Math. 601, Springer, Berlin, 1977, 149–237.Google Scholar
[LN64] Lehner, J. and Newman, M., Weierstrass points of Γ0 (n). Ann. of Math. 79(1964), 360–368.Google Scholar
[Maz77] Mazur, B., Rational points on modular curves. In: Modular Functions of One Variable. Lecture Notes in Math. 601, Springer, Berlin, 1977, pp. 107–148.Google Scholar
[Ogg74] Ogg, A. P., Hyperelliptic modular curves. Bull. Soc. Math. France 102(1974), 449–462.Google Scholar