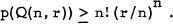Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Marcus, Marvin
and
Minc, Henryk
1965.
Permanents.
The American Mathematical Monthly,
Vol. 72,
Issue. 6,
p.
577.
Marcus, Marvin
and
Minc, Henryk
1967.
On a conjecture of B. L. van der Waerden.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 63,
Issue. 2,
p.
305.
Minc, Henryk
1967.
A lower bound for permanents of (0,1)-matrices.
Proceedings of the American Mathematical Society,
Vol. 18,
Issue. 6,
p.
1128.
King, Bruce W.
and
Parker, Francis D.
1969.
A Fibonacci Matrix and the Permanent Function.
The Fibonacci Quarterly,
Vol. 7,
Issue. 5,
p.
539.
Metropolis, N.
Stein, M.L.
and
Stein, P.R.
1969.
Permanents of cyclic (0,1) matrices.
Journal of Combinatorial Theory,
Vol. 7,
Issue. 4,
p.
291.
Hedrick, Mark Blondeau
1975.
p-Minors of a doubly stochastic matrix at which the permanent achieves a minimum.
Linear Algebra and its Applications,
Vol. 10,
Issue. 2,
p.
177.
Brualdl, Richard A.
and
Foregger, Thomas H.
1975.
Matrices with constant permanental minors†.
Linear and Multilinear Algebra,
Vol. 3,
Issue. 3,
p.
227.
Cummings, Larry J.
and
Wallis, Jennifer Seberry
1977.
An Algorithm for the Permanent of Circulant Matrices.
Canadian Mathematical Bulletin,
Vol. 20,
Issue. 1,
p.
67.
Whitehead, Earl Glen
1979.
Four-discordant permutations.
Journal of the Australian Mathematical Society,
Vol. 28,
Issue. 3,
p.
369.
Kim, Ki Hang
and
Roush, Fred W.
1979.
On a conjecture of Erdös and Rényl.
Linear Algebra and its Applications,
Vol. 23,
Issue. ,
p.
179.
Minc, Henryk
1985.
Recurrence formulas for permanents of (0, 1)-circulants.
Linear Algebra and its Applications,
Vol. 71,
Issue. ,
p.
241.
Beker, Henry
and
Mitchell, Chris
1987.
Permutations with Restricted Displacement.
SIAM Journal on Algebraic Discrete Methods,
Vol. 8,
Issue. 3,
p.
338.
Shevelev, V. S.
1992.
Some problems of the theory of enumerating the permutations with restricted positions.
Journal of Soviet Mathematics,
Vol. 61,
Issue. 4,
p.
2272.
Marcus, Marvin
2003.
Henryk Minc - A Biography.
Linear and Multilinear Algebra,
Vol. 51,
Issue. 1,
p.
1.
Salvi, Rodolfo
and
Zagaglia Salvi, Norma
2006.
On very sparse circulant (0,1) matrices.
Linear Algebra and its Applications,
Vol. 418,
Issue. 2-3,
p.
565.
Kilic, Emrah
and
Tasci, Dursun
2007.
Factorizations and representations of the backward second-order linear recurrences.
Journal of Computational and Applied Mathematics,
Vol. 201,
Issue. 1,
p.
182.
Kilic, Emrah
and
Taşci, Dursun
2007.
On the Permanents of Some Tridiagonal Matrices with Applications to the Fibonacci and Lucas Numbers.
Rocky Mountain Journal of Mathematics,
Vol. 37,
Issue. 6,
Kiliç, E.
and
Taşci, D.
2008.
On Sums Of Second Order Linear Recurrences by Hessenberg Matrices.
Rocky Mountain Journal of Mathematics,
Vol. 38,
Issue. 2,
Kilic, Emrah
2008.
Sums of the squares of terms of sequence {u n }.
Proceedings Mathematical Sciences,
Vol. 118,
Issue. 1,
p.
27.
Kılıç, Emrah
2009.
The generalized Pell (p,i)-numbers and their Binet formulas, combinatorial representations, sums.
Chaos, Solitons & Fractals,
Vol. 40,
Issue. 4,
p.
2047.
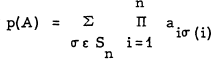
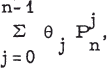 , where θj = 0 or 1, j = 1,…, n, and
Pn is the n-square permutation matrix with ones in the (1, 2),
(2, 3),…, (n-1, n), (n, 1) positions, is called a (0, 1)-circulant. Denote
the (0, 1)-circulant
, where θj = 0 or 1, j = 1,…, n, and
Pn is the n-square permutation matrix with ones in the (1, 2),
(2, 3),…, (n-1, n), (n, 1) positions, is called a (0, 1)-circulant. Denote
the (0, 1)-circulant 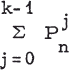 . It has
been conjectured that
. It has
been conjectured that