Published online by Cambridge University Press: 20 November 2018
We give necessary and sufficient conditions of the 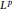 ${{L}^{p}}$-well-posedness (resp.
${{L}^{p}}$-well-posedness (resp. 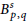 $B_{p,\,q}^{s}$-wellposedness) for the second order degenerate differential equation with finite delays
$B_{p,\,q}^{s}$-wellposedness) for the second order degenerate differential equation with finite delays
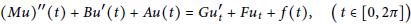 $${{\left( Mu \right)}^{\prime \prime }}\left( t \right)+B{u}'\left( t \right)+Au\left( t \right)=G{{{u}'}_{t}}+F{{u}_{t}}+f\left( t \right),\left( t\in \left[ 0,2\pi \right] \right)$$
$${{\left( Mu \right)}^{\prime \prime }}\left( t \right)+B{u}'\left( t \right)+Au\left( t \right)=G{{{u}'}_{t}}+F{{u}_{t}}+f\left( t \right),\left( t\in \left[ 0,2\pi \right] \right)$$
with periodic boundary conditions 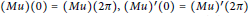 $\left( Mu \right)\,\left( 0 \right)\,=\,\left( Mu \right)\,\left( 2\pi \right),\,{{\left( Mu \right)}^{\prime }}\left( 0 \right)\,=\,{{\left( Mu \right)}^{\prime }}\left( 2\pi \right)$, where
$\left( Mu \right)\,\left( 0 \right)\,=\,\left( Mu \right)\,\left( 2\pi \right),\,{{\left( Mu \right)}^{\prime }}\left( 0 \right)\,=\,{{\left( Mu \right)}^{\prime }}\left( 2\pi \right)$, where 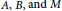 $A,\,B,\,\text{and}\,M$ are closed linear operators on a complex Banach space
$A,\,B,\,\text{and}\,M$ are closed linear operators on a complex Banach space 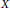 $X$ satisfying
$X$ satisfying 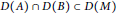 $D\left( A \right)\,\cap \,D\left( B \right)\,\subset \,D\left( M \right)$,
$D\left( A \right)\,\cap \,D\left( B \right)\,\subset \,D\left( M \right)$, 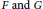 $F\,\text{and}\,G$ are bounded linear operators from
$F\,\text{and}\,G$ are bounded linear operators from 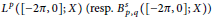 ${{L}^{p}}\left( \left[ -2\pi ,\,0 \right];\,X \right)\,\left( \text{resp}\text{.}\,\text{B}_{p,q}^{s}\left( \left[ -2\pi ,\,0 \right];\,X \right) \right)$ into
${{L}^{p}}\left( \left[ -2\pi ,\,0 \right];\,X \right)\,\left( \text{resp}\text{.}\,\text{B}_{p,q}^{s}\left( \left[ -2\pi ,\,0 \right];\,X \right) \right)$ into 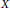 $X$.
$X$.