Article contents
Perfectly packing a cube by cubes of nearly harmonic sidelength
Published online by Cambridge University Press: 14 February 2023
Abstract
Let d be an integer greater than 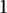 $1$, and let t be fixed such that
$1$, and let t be fixed such that  $\frac {1}{d} < t < \frac {1}{d-1}$. We prove that for any
$\frac {1}{d} < t < \frac {1}{d-1}$. We prove that for any 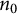 $n_0$ chosen sufficiently large depending on t, the d-dimensional cubes of sidelength
$n_0$ chosen sufficiently large depending on t, the d-dimensional cubes of sidelength 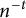 $n^{-t}$ for
$n^{-t}$ for 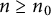 $n \geq n_0$ can perfectly pack a cube of volume
$n \geq n_0$ can perfectly pack a cube of volume 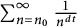 $\sum _{n=n_0}^{\infty } \frac {1}{n^{dt}}$. Our work improves upon a previously known result in the three-dimensional case for when
$\sum _{n=n_0}^{\infty } \frac {1}{n^{dt}}$. Our work improves upon a previously known result in the three-dimensional case for when 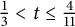 $\frac {1}{3} < t \leq \frac {4}{11} $ and
$\frac {1}{3} < t \leq \frac {4}{11} $ and 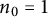 $n_0 = 1$ and builds upon recent work of Terence Tao in the two-dimensional case.
$n_0 = 1$ and builds upon recent work of Terence Tao in the two-dimensional case.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
Research of the author is partially supported by NSERC CGS-M.
References
- 2
- Cited by



