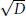Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mollin, Richard A.
and
Srinivasan, Anitha
2012.
Residuacity and genus theory of forms.
Journal of Number Theory,
Vol. 132,
Issue. 1,
p.
103.
O’Sullivan, Cormac
and
Taylor, Karen
2016.
Hyperbolic Fourier coefficients of Poincaré series.
The Ramanujan Journal,
Vol. 41,
Issue. 1-3,
p.
465.
Issa, Ahmad
Sankari, Hasan
and
Guo, Li
2020.
Some Criteria for Class Numbers to Be Non-One.
Journal of Mathematics,
Vol. 2020,
Issue. ,
p.
1.
Srinivasan, Anitha
2022.
Infinitely many sign changes of the Liouville function on 𝑋²+𝐷.
Proceedings of the American Mathematical Society,
Vol. 150,
Issue. 9,
p.
3799.