Hostname: page-component-669899f699-rg895 Total loading time: 0 Render date: 2025-04-25T12:52:44.016Z Has data issue: false hasContentIssue false
  • English
  • Français

p-Adic quotient sets: Linear recurrence sequences with reducible characteristic polynomials

Part of: Forms and linear algebraic groups Sequences and sets

Published online by Cambridge University Press:  11 December 2024

Deepa Antony Open the ORCID record for Deepa Antony [Opens in a new window]  and
Rupam Barman Open the ORCID record for Rupam Barman [Opens in a new window]
Deepa Antony
Affiliation:
Department of Mathematics, Indian Institute of Technology Guwahati, Guwahati, Assam, India, 781039 e-mail: [email protected]
Rupam Barman*
Affiliation:
Department of Mathematics, Indian Institute of Technology Guwahati, Guwahati, Assam, India, 781039 e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 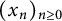$(x_n)_{n\geq 0}$ be a linear recurrence sequence of order 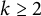$k\geq 2$ satisfying

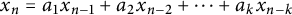$$ \begin{align*}x_n=a_1x_{n-1}+a_2x_{n-2}+\dots+a_kx_{n-k}\end{align*} $$
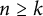for all integers $n\geq k$, where 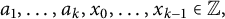$a_1,\dots ,a_k,x_0,\dots , x_{k-1}\in \mathbb {Z},$ with 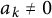$a_k\neq 0$. In 2017, Sanna posed an open question to classify primes p for which the quotient set of 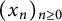$(x_n)_{n\geq 0}$ is dense in 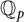$\mathbb {Q}_p$. In a recent paper, we showed that if the characteristic polynomial of the recurrence sequence has a root 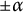$\pm \alpha $, where 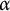$\alpha $ is a Pisot number and if p is a prime such that the characteristic polynomial of the recurrence sequence is irreducible in 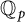$\mathbb {Q}_p$, then the quotient set of 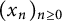$(x_n)_{n\geq 0}$ is dense in 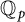$\mathbb {Q}_p$. In this article, we answer the problem for certain linear recurrence sequences whose characteristic polynomials are reducible over 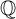$\mathbb {Q}$.

Keywords

p-Adic numberquotient setratio setlinear recurrence sequence

MSC classification

Primary: 11B05: Density, gaps, topology 11B37: Recurrences 11E95: $p$-adic theory
Type
Article
Information
Canadian Mathematical Bulletin , Volume 68 , Issue 1 , March 2025 , pp. 177 - 186
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Antony, D. and Barman, R., $p$ -adic quotient sets: Cubic forms . Arch. Math. 118(2022), no. 2, 143–149.CrossRefGoogle Scholar
Antony, D. and Barman, R., $p$ -adic quotient sets: Linear recurrence sequences . Bull. Aust. Math. Soc. (2023), 1–10.Google Scholar
Antony, D., Barman, R., and Miska, P., $p$ -adic quotient sets: Diagonal forms . Arch. Math. 119(2022), no. 5, 461–470.CrossRefGoogle Scholar
Brown, B., Dairyko, M., Garcia, S. R., Lutz, B., and Someck, M., Four quotient set gems . Amer. Math. Monthly 121(2014), no. 7, 590–599.CrossRefGoogle Scholar
Bukor, J. and Csiba, P., On estimations of dispersion of ratio block sequences . Math. Slovaca 59(2009), no. 3, 283–290.CrossRefGoogle Scholar
Bukor, J., Erdős, P., Šalát, T., and Tóth, J. T., Remarks on the $(R)$ -density of sets of numbers. II. Math. Slovaca 47(1997), no. 5, 517–526.Google Scholar
Bukor, J. and Tóth, J. T., On accumulation points of ratio sets of positive integers . Amer. Math. Monthly 103(1996), no. 6, 502–504.CrossRefGoogle Scholar
Donnay, C., Garcia, S. R., and Rouse, J., p-adic quotient sets II: Quadratic forms . J. Number Theory 201(2019), 23–39.CrossRefGoogle Scholar
Garcia, S. R., Quotients of Gaussian primes . Amer. Math. Monthly 120(2013), no. 9, 851–853.CrossRefGoogle Scholar
Garcia, S. R., Hong, Y. X., Luca, F., Pinsker, E., Sanna, C., Schechter, E., and Starr, A., $p$ -adic quotient sets . Acta Arith. 179(2017), no. 2, 163–184.CrossRefGoogle Scholar
Garcia, S. R. and Luca, F., Quotients of Fibonacci numbers . Amer. Math. Monthly 123(2016), 1039–1044.CrossRefGoogle Scholar
Garcia, S. R., Poore, D. E., Selhorst-Jones, V., and Simon, N., Quotient sets and Diophantine equations . Amer. Math. Monthly 118(2011), no. 8, 704–711.CrossRefGoogle Scholar
Gouvêa, F. Q., $p$ -adic numbers. An introduction. 2nd ed., Universitext, Springer, Berlin, 1997.CrossRefGoogle Scholar
Hedman, S. and Rose, D., Light subsets of $\mathbb{N}$ with dense quotient sets . Amer. Math. Monthly 116(2009), no. 7, 635–641.Google Scholar
Hobby, D. and Silberger, D. M., Quotients of primes . Amer. Math. Monthly 100(1993), no. 1, 50–52.CrossRefGoogle Scholar
Luca, F., Pomerance, C., and Porubský, Š., Sets with prescribed arithmetic densities . Unif. Distrib. Theory 3(2008), no. 2, 67–80.Google Scholar
Micholson, A., Quotients of primes in arithmetic progressions . Notes Number Theory Discrete Math. 18(2012), no. 2, 56–57.Google Scholar
Mišík, L., Sets of positive integers with prescribed values of densities . Math. Slovaca 52(2002), no. 3, 289–296.Google Scholar
Miska, P., A note on $p$ -adic denseness of quotients of values of quadratic forms . Indag. Math. 32(2021), 639–645.CrossRefGoogle Scholar
Miska, P., Murru, N. and Sanna, C., On the p-adic denseness of the quotient set of a polynomial image . J. Number Theory 197(2019), 218–227.CrossRefGoogle Scholar
Miska, P. and Sanna, C., $p$ -adic denseness of members of partitions of $\mathbb{N}$ and their ratio sets . Bull. Malays. Math. Sci. Soc. 43(2020), no. 2, 1127–1133.CrossRefGoogle Scholar
Rawashdeh, E. A., A simple method for finding the inverse of Vandermonde matrix . Mat. Vesn. 71(2019), no. 3, 207–213.Google Scholar
Rosen, K. H., Discrete Mathematics and Its Applications . McGraw-Hill Education, 2011.Google Scholar
Šalát, T., On ratio sets of natural numbers . Acta Arith. 15(1968/1969), 273–278.CrossRefGoogle Scholar
Šalát, T., Corrigendum to the paper “On ratio sets of natural numbers”. Acta Arith. 16(1969/1970), 103.Google Scholar
Sanna, C., The quotient set of k-generalized Fibonacci numbers is dense in ${\mathbb{Q}}_p$ . Bull. Aust. Math. Soc. 96(2017), no. 1, 24–29.CrossRefGoogle Scholar
Sittinger, B. D., Quotients of primes in an algebraic number ring . Notes Number Theory Discrete Math. 24(2018), no. 2, 55–62.CrossRefGoogle Scholar
Starni, P., Answers to two questions concerning quotients of primes . Amer. Math. Monthly 102(1995), no. 4, 347–349.CrossRefGoogle Scholar
Strauch, O. and Tóth, J. T., Asymptotic density of $A\subset \mathbb{N}$ and density of the ratio set $R(A)$ . Acta Arith. 87(1998), no. 1, 67–78.CrossRefGoogle Scholar